| Empfehlungen |  |

Eingleichungsmodell-Schätzung
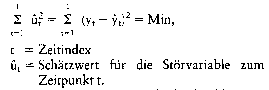 mit o2 = Varianz der Störvariablen. Sind die ut unkorreliert, so erfolgt die Bestimmung der Regressionskoeffizienten durch Maximierung der gemeinsamen Dichtefunktion (,,Likelihood"-Funktion): mit o2 = Varianz der Störvariablen. Sind die ut unkorreliert, so erfolgt die Bestimmung der Regressionskoeffizienten durch Maximierung der gemeinsamen Dichtefunktion (,,Likelihood"-Funktion): 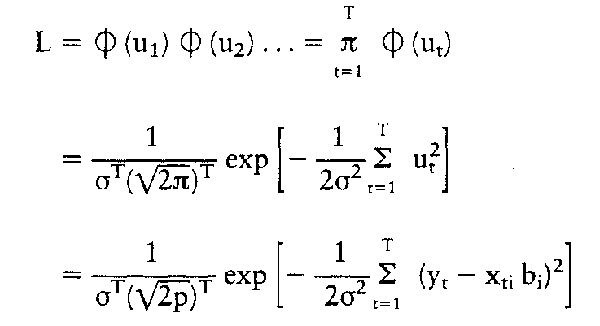 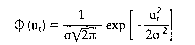 Im Gegensatz zur Methode der kleinsten Quadrate benötigt man zur Anwendung der Maximum-Likelihood-Methode eine Annahme über die Verteilung der Störvariablen ut. Nimmt man Normalverteilung an, so lautet die Dichtefunktion für die Variable ut: für i = 1, 2,... n Mit Hilfe der verallgemeinerten Methode der kleinsten Quadrate ("Aitken"-Schätzung) ist es schliesslich möglich, auch Eingleichungs- modelle mit autokorrelierten und streuungsvariablen Störgrössen zu schätzen. Literatur: Hübler, O., Ökonometrie, Stuttgart, New York 1989. Im Gegensatz zur Methode der kleinsten Quadrate benötigt man zur Anwendung der Maximum-Likelihood-Methode eine Annahme über die Verteilung der Störvariablen ut. Nimmt man Normalverteilung an, so lautet die Dichtefunktion für die Variable ut: für i = 1, 2,... n Mit Hilfe der verallgemeinerten Methode der kleinsten Quadrate ("Aitken"-Schätzung) ist es schliesslich möglich, auch Eingleichungs- modelle mit autokorrelierten und streuungsvariablen Störgrössen zu schätzen. Literatur: Hübler, O., Ökonometrie, Stuttgart, New York 1989.
Vorhergehender Fachbegriff: Eingetragener Verein (e.V.) | Nächster Fachbegriff: Eingleichungsmodelle Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken |
|
Schreiben Sie sich in unseren kostenlosen Newsletter ein
Bleiben Sie auf dem Laufenden über Neuigkeiten und Aktualisierungen bei unserem Wirtschaftslexikon, indem Sie unseren monatlichen Newsletter empfangen. Garantiert keine Werbung. Jederzeit mit einem Klick abbestellbar.
Weitere Begriffe : Gewerkenbuch | Bauklassenverfahren | Flexible Sollkostenvorgabe
|
Praxisnahe Definitionen Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar. |
Fachbegriffe der Volkswirtschaft Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre. |
Beliebte Artikel Bestimmte Erklärungen und Begriffsdefinitionen erfreuen sich bei unseren Lesern ganz besonderer Beliebtheit. Diese werden mehrmals pro Jahr aktualisiert. |
