Kontraktkurve

gibt an, bei welchen Lösungen das Pareto- Optimum erfüllt ist (kein Individuum erleidet gegenüber dem bisherigen Zustand Nutzeneinbussen) und bei welchen Lösungen deshalb ein Kontrakt Zustandekommen kann. Die Wohlfahrtsökonomik geht bei der Entwicklung der Kontraktkurve von der grundlegenden Erkenntnis aus, dass bei Tauschvorgängen und Verhandlungen der eine Tauschpartner nicht nur auf Kosten des anderen Tauschpartners Vorteile erreichen kann, sondern dass oftmals Änderungen in den Kaufbedingungen zum Vorteil beider Partner führen. So können sich die Tarifpartner bei ihren Verhandlungen beiderseitige Vorteile erhoffen, wenn die Löhne gegenüber dem bisherigen Zustand erhöht werden. Für die Arbeitnehmer bedeuten Lohnsteigerungen Einkommensvorteile, für die Arbeitgeber kann die Zustimmung zu Lohnsteigerungen vorteilhaft sein, weil damit die Gefahr eines Streiks und der hiermit verbundenen Kosten abgewendet wird oder, weil bei einer Produktivitätssteigerung, die nicht zu Lohnsteigerungen führt, die Gefahr besteht, dass andere Unternehmungen versuchen, die Produktion auszuweiten und Arbeitskräfte abzuwerben. Die Kontraktkurve wird üblicherweise in einem Diagramm dargestellt, auf deren Koordinatenachsen die zur Verfügung stehenden Mengen zweier Güterarten abgetragen werden (vgl. Abb.). Zunächst werden die sog. Indifferenzkurven eingezeichnet, die angeben, welche Güterkombinationen die einzelnen Haushalte als gleichwertig ansehen und welche im Vergleich zu anderen Kombinationen höher bewertet werden. Formal gesehen entsteht die Kontraktkurve dadurch, dass man alle Berührungspunkte zweier Indifferenzkurven miteinander verbindet. Auf der Kontraktkurve liegen alle möglichen Lösungen, bei denen alle beiderseitigen Verhandlungsvorteile bereits ausgeschöpft sind. Dies bedeutet, dass ein Weiterverhandeln solange für beide Seiten zweckmässig ist, wie die Kontraktkurve noch nicht erreicht ist. Bei Erreichen der Kontraktkurve kann jedoch ein Tausch- oder Verhandlungspartner seinen Vorteil nur noch auf Kosten des anderen Partners vergrössern. Bei welchem Punkt der Kontraktkurve schliesslich ein Tausch (Kontrakt) zustandekommt, hängt wesentlich davon ab, bei welchen Bedingungen die Verhandlungen begonnen haben. Literatur: Rose, K., Theorie der Aussenwirtschaft, 9. Aufl., München 1986. Schneider, H., Mikroökonomie. Einführung in die Preis-, Produktions- und Wohlfahrtstheorie, 4. Aufl., München 1986. Schumann, J., Grundzüge der mikroökonomischen Theorie, 5. Aufl., Berlin u. a. 1987.

geometrischer Ort effizienter Tauschsituationen oder Allokationen.
1. In der Preistheorie: Beim isolierten Tausch zwischen zwei Wirtschaftssubjekten, die beide über eine bestimmte Erstausstattung mit zwei Gütern verfügen (Abb. 1: Wirtschaftssubjekt 1 über die Menge al des Gutes A und bi des Gutes B, Wirtschaftssubjekt 2 über die Menge a2 und b2), ist die Kontraktkurve die Verbindungslinie zwischen Tangentialpunkten von Indifferenzkurven beider Wirtschaftssubjekte. Die Kontraktkurve wird in einem Boxdiagramm (EDGEWORTH-Box nach Francis Y. EDGEWORTH, 1881) dargestellt. Die Seitenlängen des Boxdiagramms sind gleich den Mengen A und B, über die beide Wirtschaftssubjekte insgesamt verfügen (al plus a2 bzw. b1 plus b2). Die Mengen des Wirtschaftssubjekts 1 werden von 01 (Koordinatensystem O\'A\'B\'), die des Wirtschaftssubjekts 2 von 02 aus (Koordinatensystem 02A2B2) gemessen. Jeder Punkt innerhalb oder am Rande des Boxdiagramms zeigt die Verteilung der insgesamt verfügbaren Gütermengen auf beide Wirtschaftssubjekte; Punkt E die Verteilung der Ausgangsmengen (Abb. 1).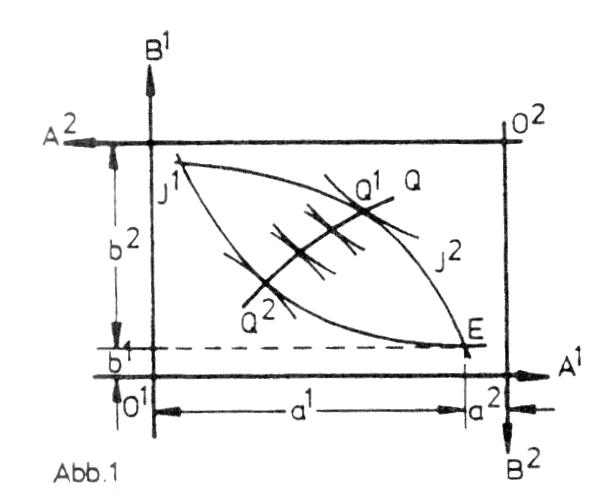
Kontraktkurve

Die Indifferenzkurve II bzw. I2 der Wirtschaftssubjekte 1 bzw. 2 kennzeichnet alle Mengenkombinationen von a und b, welche dem Wirtschaftssubjekt 1 bzw. 2 das gleiche Nutzenniveau wie die Erstausstattung stiften. Jeder Punkt innerhalb der durch beide Indifferenzkurven abgegrenzten Ebene stellt ein höheres Nutzenniveau für beide Wirtschaftssubjekte dar. Als Ergebnis von Verhandlungen zwischen den Wirtschaftssubjekten über Preis und auszutauschende Mengen (des Kontrakts) kommen nur Tangentialpunkte von Indifferenzkurven infrage, die innerhalb oder am Rande der Ebene liegen. Ihre Gesamtheit ergibt die Kontraktkurve Q; die Endpunkte Q\' bzw. Q2 stellen die Ausbeutungspunkte des Wirtschaftssubjekts 1 bzw. 2 dar (weil nur das Wirtschaftssubjekt 1 bzw. 2 auf ein höheres Versorgungsniveau gelangt).
2. In der -› Wohlfahrtökonomik: Verbindungslinie zwischen Tangentialpunkten von Indifferenzkurven zweier Wirtschaftssubjekte in einem Boxdiagramm. Die Tangentialpunkte bezeichnen solch eine Verteilung einer gegebenen Menge der Güter A und B, dass ein Wirtschaftssubjekt auf ein höheres Nutzenniveau nur zu Lasten des Nutzenniveaus des anderen gelangen kann (Abb. 2). Jeder Punkt auf der Kontraktkurve stellt daher ein - PARETOOptimum dar. Aus der Kontraktkurve wird die Nutzenmöglichkeitskurve abgeleitet.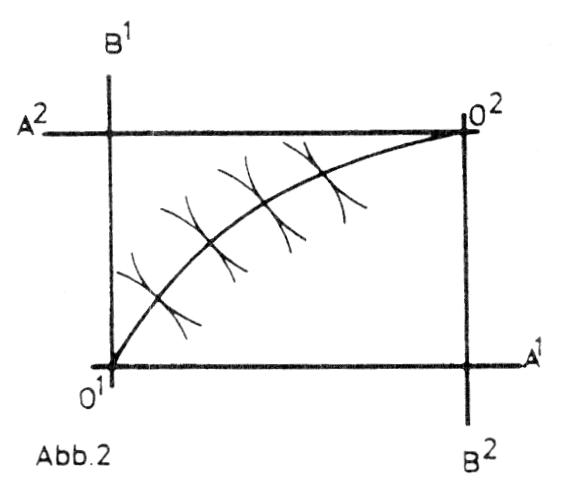

Bei Anwendung wohlfahrtsökonomischer Überlegungen auf die Produktion ist die Kontraktkurve als Verbindungslinie zwischen Tangentialpunkten von Isoquanten für zwei Produkte definiert. Die Tangentialpunkte zeigen, wie eine gegebene Menge zweier Produktionsfaktoren auf die Produktion zweier Güter aufgeteilt werden kann, so dass die Erzeugung eines Gutes nur zu Lasten des anderen erhöht werden kann. Jeder Punkt einer solchen Kontraktkurve erfüllt die für ein PARETO-Optimum notwendige Bedingung für Effizienz im Produktionsbereich. Literatur: Linde, R (1992). Schumann, J. (1992). Sohmen, E. (1976)

Vorhergehender Fachbegriff: Kontraktgröße | Nächster Fachbegriff: Kontraktlogistik

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Verbringungsort | Enquete | LEONTIEF-Paradox

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer