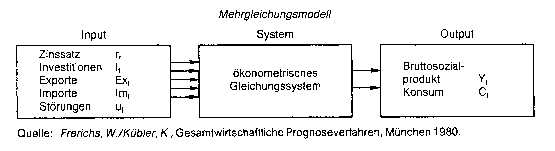Mehrgleichungsmodell

besteht aus zwei oder mehreren Gleichungen, die miteinander verknüpft sind, Ein einfaches Mehrgleichungsmodell ist z.B. durch eine Konsumfunktion und eine Definitionsgleichung gegeben: C_t = bi + b₂ Y_t + b₃ r_t + u_t Y_t = C_t + I_t + Ex_t - Im_t C_t = Konsum Y_t = Bruttosozialprodukt r_t = Zinssatz I_t = Investition Ex_t = Export Im_t = Import Das Gleichungssystem ist dadurch gekennzeichnet, dass zwischen Y_t und C_t eine wechselseitige Beziehung vorliegt: Y_tC_t

C_t und Y_t sind dabei endogene; r_t, I_t, Ex_t und Im_t sind in diesem Gleichungssystem exogene Variablen (vgl. Abb.). Mehrgleichungsmodelle sind statisch oder dynamisch. Statische Systeme liegen dann vor, wenn sich die endogenen Variablen stets auf die gleiche Periode beziehen, dynamische Modelle enthalten verzögerte Werte der endogenen Variablen y_t_i, y_t_₂, ... Betrachtet man die Koeffizientenstruktur des ökonometrischen Mehrgleichungsmodelles, so kann man zwischen interdependenten und rekursiven Systemen unterscheiden.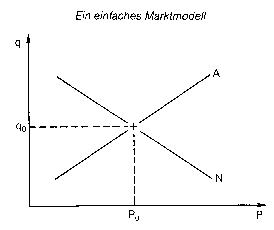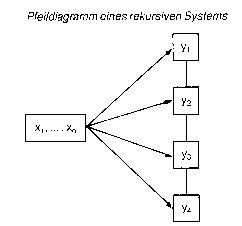

In einem rekursiven System wird die in der ersten Gleichung bestimmte endogene Variable in der zweiten Gleichung als erklärende Grösse verwendet, die in der zweiten Glei dritten Gleichung als exogene berücksichtigt, usw. (vgl. Abb.). In interdependenten Modellen liegt eine wechselseitige Verknüpfung zwischen den endogenen Variablen des Systems vor, wie etwa in folgendem Zwei-Gleichungssystem: yit = bn + gi₂ yit + bn x_2t + uit y_2t = b₂i + g₂i yit + b₂₃ x_3t + u_2t Bei interdependenten Modellen tritt oft das Problem auf, dass es nicht eindeutig möglich ist, zwischen zwei alternativen Strukturen zu entscheiden. Solche Strukturen heissen äquivalent. Wenn äquivalente Strukturen vorliegen, so ist das betreffende Modell nicht identifizierbar. Ein einfaches Marktmodell kann wie folgt formuliert werden (vgl. Abb.). q = b_n + b₁₂p + u_q p = b₂i + b₂₂ q + u_p q = Menge p = Preis Das Wertepaar (q₀p₀) ist die einzige empirische Information; aus dieser allein sind jedoch die Parameter bn nicht eindeutig zu bestimmen. Durch lineare Transformation las- die alle durch (q₀p₀) gehen. Es sind also beliebig viele äquivalente Strukturen denkbar, damit ist das Gleichungssystem nicht identifizierbar. Literatur: Frerichs, W./Kübler, K., Gesamtwirtschaftliche Prognoseverfahren, München 1980. Hu- jer, R./Cremer, R., Methoden der empirischen Wirtschaftsforschung, München 1978. Schneeweiss, H., Ökonometrie, 4. Aufl., Heidelberg 1990.

Vorhergehender Fachbegriff: Mehrgeschosslager | Nächster Fachbegriff: Mehrgleichungsmodell-Schätzung

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Appetenzkonflikt | Kreditrestriktion | Kaskoversicherung

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer