Singulärprognose

Vorhersage aufgrund einzelner Gleichungen; erfolgt im wesentlichen auf der Grundlage von Informationen Singulärprognose über die Vergangenheitsentwicklung der zu prognostizierenden Grösse. Die bekannteste Methode ist die Trendextrapolation. Die Entwicklung einer Variablen y_t wird dabei durch die Zeit t erklärt: yt = f(t) + ut f(t) = Trend u_t = Restgrösse

Je nach der Form des zeitlichen Entwicklungsprozesses der Variablen y_t wird eine lineare Trendfunktion oder andere Funktionsformen, wie z. B. geschätzt und der Prognosewert y" in Abhängigkeit von tP (z.B. 1992) ermittelt. Das Problem der Trendextrapolation besteht vor allem darin, dass Strukturkonstanz der geschätzten Parameter unterstellt werden muss.

Vor allem für kurzfristige Prognosen werden autoregressive Ansätze der Form oder die allgemeiner formulierten Box-Jenkins-Modelle angewendet. Im Gegensatz dazu werden im ökonometrischen Eingleichungsmodell Kausalzusammenhänge berücksichtigt. Die Prognose erfolgt dabei auf der Grundlage einer Erklärung der zu prognostizierenden Variablen y_t durch exogene Variablen x_it:

Die Güte der Prognose y" wird nicht nur durch die Qualität der Koeffizientenschätzung und der Stabilität der Parameter bestimmt, sondern hängt auch ganz entscheidend von der Güte der Prognosewerte für die exogenen Variablen x_it ab. Der bedeutsamste Nachteil aller Singulärprognosen besteht in der Vernachlässigung interdependenter Wirkungszusammenhänge, z. B. mit anderen endogenen Variablen y_2t, y_3t .; als wichtigster Vorteil ist die einfache Anwendbarkeit zu nennen.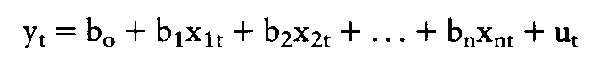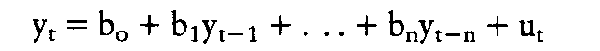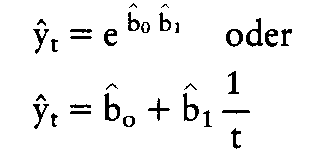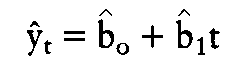

Literatur:
* Frerichs, W., Gesamtwirtschaftliche Prognoseverfahren, München.
* Weber, K., Wirtschaftsprognostik, München 1990.

Vorhergehender Fachbegriff: Singularinstanz | Nächster Fachbegriff: Singulärquellen-Verfahren

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Stückakkord | Graphische Optimierung | Systemprognose

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer