exponentielles Wachstum

Wachstumsverlauf, bei dem die Wachstumsrate, also das Verhältnis aus der absoluten Veränderung einer Variablen in der Zeit Y = dY/dt und ihrem Niveau Y(t), zu jedem betrachteten Zeitpunkt einer Funktion r(t) folgt:
exponentielles Wachstum

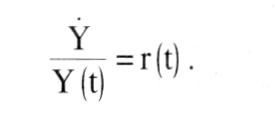Die Lösung dieser Differentialgleichung erster Ordnung lautet für einen Anfangswert Yo:
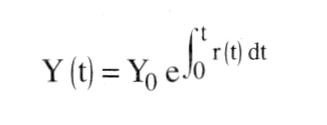exponentielles Wachstum

Für den ökonomisch oft relevanten Fall, dass die Funktion r(t) konstant ist, gilt die einfache Lösung Häufig wird eine halblogarithmische Darstellungsweise vorgezogen. Logarithmieren des Wachstumspfades ergibt:
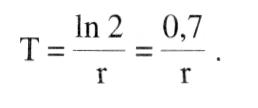exponentielles Wachstum

In einer halblogarithmischen Darstellung ergibt sich somit ein linearer Verlauf des Wachstumspfades mit der Steigung p.
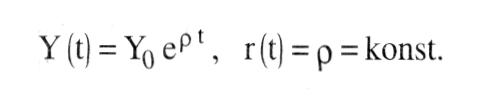exponentielles Wachstum

Bei konstanter Wachstumsrate läßt sich das exponentielle Wachstum durch die Zeit charakterisieren, die zur Verdopplung des Niveaus der betrachteten Variablen benötigt wird (Verdopplungszeit T):
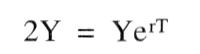exponentielles Wachstum

Daraus folgt:
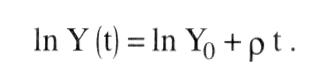exponentielles Wachstum

In der graphischen Darstellung ergibt sich folgendes Aussehen des Wachstumspfades: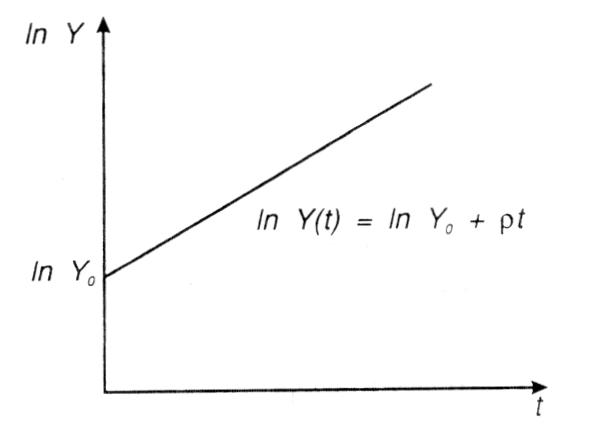

Beträgt die Wachstumsrate beispielsweise 5%, ergibt sich eine Verdopplungszeit von 14 Jahren. In den Wachstumsmodellen der modernen - Wachstumstheorie ergibt sich exponentielles Wachstum als typisches Verlaufsmuster für steady state Wachstum. Auch in der Realität lassen sich Wachstumsprozesse durch diesen Wachstumsverlauf beschreiben. Insbes. bei natürlichen Wachstumsprozessen ist aber festzustellen, dass exponentielles Wachstum nur Ausschnitte des Wachstumspfades charakterisiert. Oft ergeben sich Grenzen des Wachstums, die zu einer Abflachung des Verlaufs führen.

Vorhergehender Fachbegriff: Exponentielle Glättung | Nächster Fachbegriff: Export

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Grünes Kennzeichen | Plakatwerbung | Wertansatz

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer