FOLK-Theorem

besagt, dass jeder machbare Auszahlungsvektor eines Ein-Perioden-Spiels als teil-spielperfektes (NASH-)Gleichgewicht in jeder Periode realisiert werden kann, ohne dass die Spieler verbindliche Abmachungen treffen, sofern das Ein-Perioden-Spiel ohne vorhersehbares Ende (mit unbeschränktem Zeithorizont) wiederholt wird und die Spieler die Summe der (Nutzen-) Auszahlungen aus jedem Teilspiel über alle Perioden maximieren (Spieltheorie).
FOLK-Theorem

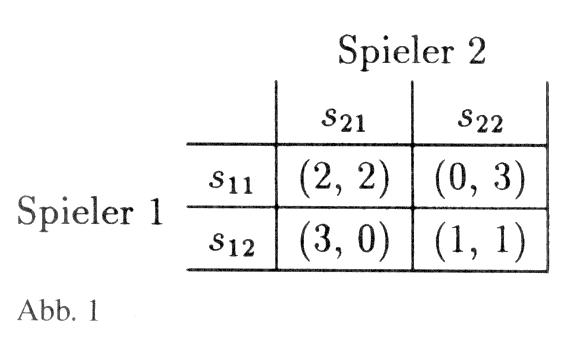Zur Illustration eignet sich das in Abb. 1 dargestellte Gefangenendilemma. Können sich die Spieler in diesem nicht verpflichten, ihre ersten Strategien zu spielen, und wird das Spiel nur einmal gespielt, dann werden sie ihre zweiten Strategien wählen, denn diese sind dominante Strategien (stochastische Dominanz ersten Grades), und das PARETO-inferiore Ergebnis (1, 1) resultiert. Wird das Gefangenendilemma aber mit unendlichem Zeithorizont wiederholt (iteriert) und maximieren die Spieler die Summe der abdiskontierten Nutzen, so impliziert z.B. die Strategienkombination s* = (s11, s21) für jede Periode und damit auch für das iterierte Spiel ein teilspielperfektes Gleichgewicht, wenn ein Spieler in den nachfolgenden Perioden stets seine zweite Strategie wählt, falls der Mitspieler nicht seine erste Strategie wählt. Weicht ein Spieler von s* ab, dann steht einem einmaligen Nutzengewinn von 3 — 2 = 1 eine Einbuße von 2 — 1 = 1 gegenüber. Da diese Einbuße über unendlich viele Perioden aufsummiert wird, ist sie auch dann größer, wenn wir ein Gefangenendilemma mit anderen Zahlenwerten betrachten. Aber nicht nur das PARETO-optimale Auszahlungspaar (2, 2) wird in jeder Periode durch ein NASH-Gleichgewicht unterstützt. 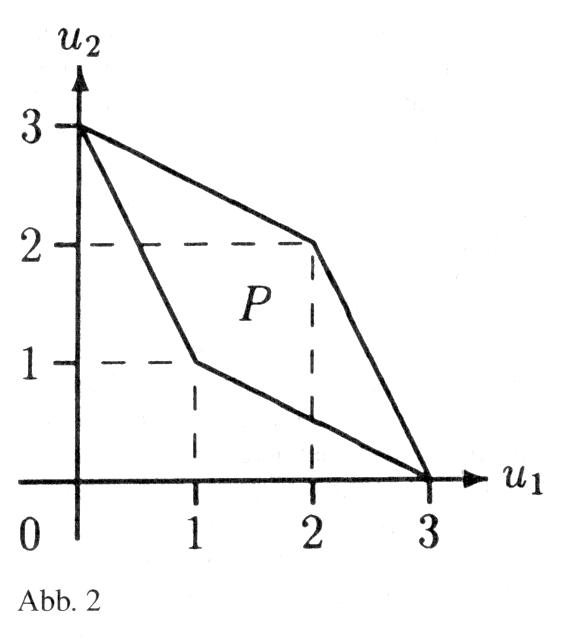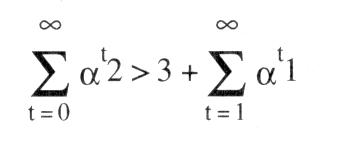Das FOLK-Theorem besagt, dass jedes Auszahlungspaar in der »konvexen Hülle« P der Punkte (2, 2), (0, 3), (3, 0) und (1, 1) durch ein NASH-Gleichgewicht implementiert werden kann, wenn das Spiel mit unbegrenztem Zeithorizont wiederholt wird. Die »konvexe Hülle« P der Punkte (2, 2), (0, 3), (3, 0) und (1, 1) ist die geschlossene Menge aller Punkte, deren Rand aus Verbindungslinien dieser vier Punkte besteht (Abb. 2). Diskontieren die Spieler ihre zukünftigen Nutzen ab, so wird das Auszahlungspaar (2, 2) trotzdem durch ein NASH-Gleichgewicht unterstützt, wenn für jeden der beiden Spieler die Summe der abdiskontierten Nutzen größer ist als der Nutzengewinn, den er erzielte, wenn er statt seiner ersten seine zweite Strategie spielte und der andere Spieler zunächst seine erste Strategie und dann stets seine zweite wählte. Für das Beispiel in Abb. 1 folgt als Bedingung: bzw.
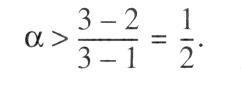FOLK-Theorem

Hierbei ist a der Diskontfaktor, der aus a = 1/(1+r) folgt, falls r den a-internen Zinssatz des jeweiligen Spielers wiedergibt. Voraussetzung für die a-Implementierung von (2, 2) ist, dass auch bei Abdiskontierung das Ein-Perioden-Spiel mit unbeschränktem Zeithorizont wiederholt wird. Wäre der Zeithorizont beschränkt, träfe das chain-store-Paradoxon (Ladenkettenparadoxon) zu und in jedem Teilspiel wäre mit dem PARETO-inferioren Auszahlungsvektor (I, 1) zu rechnen. In der letzten Periode (T) wählt jeder Spieler seine dominante, d.h. seine zweite Strategie, und es resultiert (1, 1). Damit haben die Entscheidungen in der Vorperiode (T-1) keinen Einfluss auf die Entscheidung in T. Jeder Spieler wird deshalb auch in dieser Periode seine zweite Strategie wählen, und wiederum resultiert das Auszahlungspaar (1, 1). Damit haben die Entscheidungen in der Periode T-2 keinen Einfluss auf die Entscheidungen in der Periode T-1; jeder Spieler wird deshalb seine zweite Strategie wählen, und es resultiert wiederum (1, 1). Durch Rückwärtsinduktion bis zur Periode 1 kommen wir zu dem Schluß, dass die Entscheidungen in der Periode 1 keinen Einfluss auf die Entscheidungen in der Periode 2 haben und deshalb jeder Spieler bereits in Periode 1 seine zweite Strategie wählen wird. Damit resultiert in jeder Periode bzw. in jedem Teilspiel das PARETO-inferiore Auszahlungspaar (1, 1).
FOLK-Theorem

Literatur: Holler, M.J. (1992). Holler, M.L., Illing, G. (1991). Friedman, J.W. (1986)

Vorhergehender Fachbegriff: Folgewirkungen | Nächster Fachbegriff: FOMC

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Realeinkommen | Marktplatz, elektronischer | Placierung

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer