| Empfehlungen |  |

Lineares Gleichungssystem
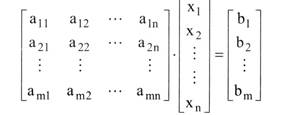 Soweit ein Gleichungssystem eine eindeutige Lösung besitzt, kann diese mithilfe des Gauss\'schen Eliminationsverfahrens bestimmt werden. Dabei werden einzelne Gleichungen Soweit ein Gleichungssystem eine eindeutige Lösung besitzt, kann diese mithilfe des Gauss\'schen Eliminationsverfahrens bestimmt werden. Dabei werden einzelne Gleichungen (1) vertauscht, (2) mit reellen Zahlen # 0 multipliziert oder (3) addiert bzw. voneinander subtrahiert, um eine (obere oder untere) Dreiecksmatrix zu erzeugen. Liegt eine Dreiecksmatrix vor, können die gesuchten Unbekannten xl, x2,..., xn durch Rückwärtseinsetzen sukzessive berechnet werden. Siehe auch Wirtschaftsmathematik (mit Literaturangaben). siehe lineares Gleichungssystem. Siehe auch Wirtschaftsmathematik (mit Literturangaben). Vorhergehender Fachbegriff: linearer Kostenverlauf | Nächster Fachbegriff: lineares Optimierungsmodell Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken |
|
Schreiben Sie sich in unseren kostenlosen Newsletter ein
Bleiben Sie auf dem Laufenden über Neuigkeiten und Aktualisierungen bei unserem Wirtschaftslexikon, indem Sie unseren monatlichen Newsletter empfangen. Garantiert keine Werbung. Jederzeit mit einem Klick abbestellbar.
Weitere Begriffe : Lagersteuerung | Risikoaversion | Versicherungsfremde Leistungen
|
Praxisnahe Definitionen Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar. |
Fachbegriffe der Volkswirtschaft Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre. |
Beliebte Artikel Bestimmte Erklärungen und Begriffsdefinitionen erfreuen sich bei unseren Lesern ganz besonderer Beliebtheit. Diese werden mehrmals pro Jahr aktualisiert. |
