Homothetie

Eigenschaft von Funktionen, die in der Produktions-, Nutzen- und Wohlfahrtstheorie von Bedeutung sind. Homothetie kann als Verallgemeinerung des Konzepts der -i Homogenität aufgefaßt werden. Eine Funktion y = y (x1,..., xm) ist homothetisch, wenn sie als Funktion f einer linear-homogenen Funktion g geschrieben werden kann.

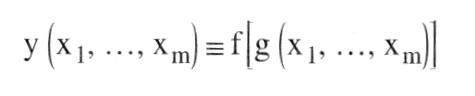Homothetie einer Produktionsfunktion impliziert, dass alle - Isoquanten im Schnittpunkt mit einem Ursprungsstrahl (z.B. Strahl I oder II in der Abb.) die gleiche Steigung aufweisen. Das kostenminimierende Verhältnis der FaktoreinSatzmengen ist bei Homothetie unabhängig vom Produktionsniveau. Bei geeigneter Wahl der Funktion f kann die Skalenelastizität entlang einem Strahl I oder II variieren. Anders als Homogenität läßt Homothetie einer Produktionsfunktion zunächst increasing returns to scale, später decreasing returns to scale zu. Nutzenfunktionen mit der Eigenschaft der Homothetie haben Indifferenzkurven von analogem Aussehen (Abb.). Die zugehörige - Einkommen-Konsum-Kurve ist ein Ursprungsstrahl, und sämtliche Einkommenselastizitäten der Nachfrage sind Eins. Die Homothetie-Eigenschaft ist für Nutzenfunktionen somit nur begrenzt realistisch. Gleichwohl werden sie besonders zur Abbildung gesellschaftlicher Nutzenschätzungen (Wohlfahrtsfunktion) u.a. in der Außenhandelstheorie nicht selten verwendet. Literatur: Hesse, H., Linde, R. (1976a)

Vorhergehender Fachbegriff: Homoskedastizität | Nächster Fachbegriff: Hong Kong Exchange and Clearing Limited

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : exponentielle Glättung | Akzessorische Sicherheiten | Bilanzkontrollgesetz (BilKoG)

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer