Nicht-Nullsummenspiel

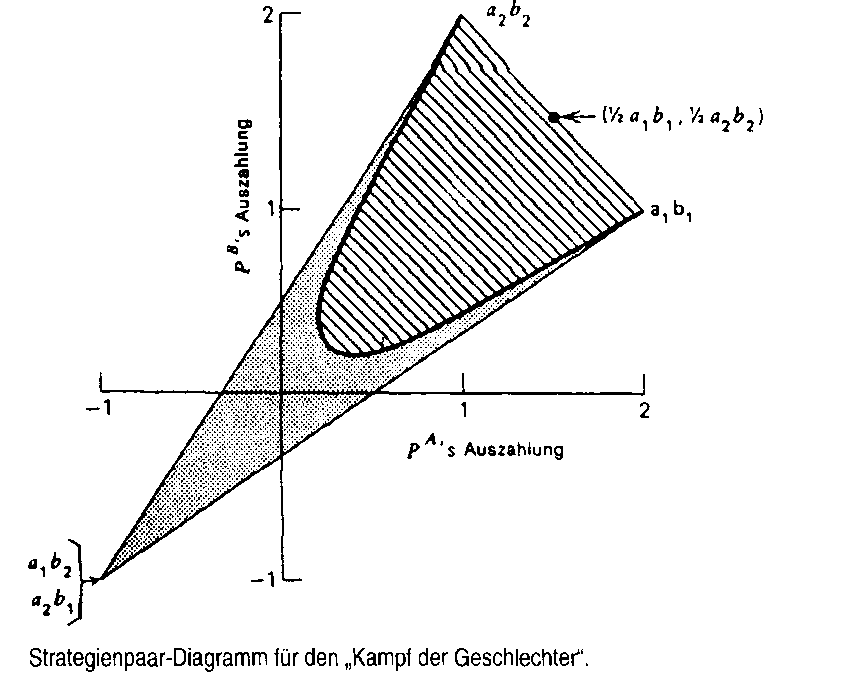Das in der Spieltheorie erdachte Nullsummenspiel hat sich als kein passendes Modell für Interaktionen im realen Leben erwiesen. Daher ist die Spieltheorie auf Nicht-Nullsummenspiele und besonders auf solche partiell wettbewerblicher Natur erweitert worden.

Die Nicht-Nullsummenspiele sind idealtypisch in verhandelbare und nichtverhandelbare Spiele unterteilt worden; der Unterschied liegt in der Art der Spieldurchführung: Bei verhandelbaren Spielen (Kooperationsspiel) ist vor dem Spiel eine Verständigung der Kontrahenten miteinander zulässig, in deren Verlauf die Spieler vielleicht zu einer Einigung über ihr jeweiliges Verhalten - die dann bindend ist - kommen. Die Vereinbarung ist einer geschäftlichen Abmachung oder einem Vertrag vergleichbar. Bei nichtverhandelbaren Spielen (Nicht-Kooperationsspielen) muss der Spieler seine Entscheidung ohne vorherige Abmachung mit dem Mitspieler oder vorherige Kenntnis von dessen Absichten treffen.
Im Strategienpaar-Diagramm kann jedes Strategienpaar arbj als Punkt dargestellt werden: Die Abszisse repräsentiert die Auszahlung bzw. erwartete Auszahlung für PA bei diesem Strategienpaar, die Ordinate stellt die entsprechende Konsequenz für PB dar.
Die Matrix stammt von Luce & Raiffa, die sie als repräsentativ für den “Kampf der Geschlechter” interpretieren: PA und PB sind ein Mann und eine Frau, die sich beide entscheiden müssen, ob sie zu einem Boxkampf oder ins Ballett gehen wollen. Der Mann bevorzugt den Boxkampf, die Frau das Ballett. Jeder von beiden würde jedoch noch lieber gemeinsam zu der nicht bevorzugten als alleine zu der bevorzugten Veranstaltung gehen. Die Strategienpaare a1b2 und a2b1 führen zu den gleichen Auszahlungen und werden daher im Diagramm durch den gleichen Punkt dargestellt; solche Paare werden als äquivalent bezeichnet. Paare randomisierter gemischter Strategien können in dem Diagramm gleichfalls dargestellt werden, doch es muss sich nicht um eine konvexe Menge handeln. In der Abbildung enthält der gepunktete Bereich mit seinen Begrenzungslinien alle reinen und alle zufallsgesteuerten gemischten Strategien, die den Spielern PA und PB in einem nichtverhandelbaren Spiel verfügbar sind.

Jede gemischte Strategie, die in einem nichtverhandelbaren Spiel gewählt werden kann, ist auch in einem verhandelbaren Spiel verfügbar - die Spieler können sich darauf einigen, jedes reine oder gemischte Strategienpaar zu spielen, das sie auch ohne Absprache hätten spielen können. Darüber hinaus ermöglicht das Verhandeln die Berücksichtigung von Strategienpaaren, die unter der Bedingung der Nicht-Verhandelbarkeit unmöglich wären. Diese neuen Strategienpaare stellen - korrelierte gemischte Strategien dar. Sie sind gemischt, weil die Strategie eines Spielers die Wahl von mehr als einer Alternative als Möglichkeit einschließt, und sie sind korreliert, weil die Entscheidungen beider Spieler in einem Durchgang nicht unabhängig voneinander getroffen werden.
Das bekannteste und am intensivsten untersuchte partiell wettbewerbliche Spiel ist das Häftlingsdilemma (Prisoner\'s Dilemma Game - PDG).

Vorhergehender Fachbegriff: Nicht-lineare Sollkostenfunktion | Nächster Fachbegriff: Nicht-Regierungsorganisationen

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Hinterbliebenenbeihilfe | Streckengeschäft | Franc de la Communaute Financiere Africaine

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer