adaptives Filtern

Idee und Bezeichnung stammen aus der Elektrotechnik; sie wurden erst im Laufe der 70er Jahre auf Prognoseprobleme übertragen. Das Hauptziel besteht in der Vorhersage von künftigen Werten einer Zeitreihe mit Hilfe ihrer Vergangenheitswerte. Spezifisch für das Adaptive Filtern ist dabei, dass die Vergangenheitswerte nicht starr, wie dies z.B. bei der Methode der gleitenden Durchschnitte oder bei der exponentiellen Glättung der Fall ist, sondern adaptiv gewichtet werden.
Werden p Vergangenheitswerte zur Vorhersage einer Grösse X verwendet, so lässt sich das Prognoseproblem folgendermassen formalisieren: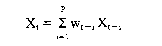
adaptives Filtern

Dabei symbolisieren w die Gewichte und t den Zeitindex. Die Berechnung der Gewichte ist nur auf iterativem Wege möglich. Vorgegebene Startgewichte werden mit Hilfe eines Gradientenverfahrens (Widrow-Hoff-Algorithmus) so lange verbessert, bis die Summe der quadrierten Abweichungen zwischen den errechneten und beobachteten Werten der Zeitreihe ein Minimum erreicht. Eine Weiterentwicklung des einfachen adaptiven Filterns stellt das generalisierte adaptive Filtern dar, bei dem neben autoregressiven Prozessen simultan auch Moving-Average-Prozesse unterstellt werden.

Variante der autoregressiven Verfahren im Rahmen der Absatzprognose, die nur die tatsächlichen Zeitreihenwerte benutzt, um das zukünftige Verhalten einer Zeitreihe zu prognostizieren. Das adaptive Filtern legt dieselbe Prognosegleichung zugrunde wie das Box-Jenkins-Verfahren: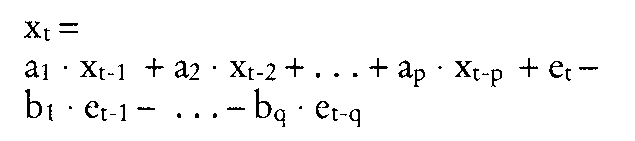
Adaptives Filtern

(x = Zeitreihenwerte, e = Störvariable, a und b zu schätzende Parameter)

Die beiden Verfahren unterscheiden sich allerdings bei der Schätzung der Modellparameter a; und b: während Box/Jenkins ein nicht-lineares Gleichungssystem verwenden, begnügt man sich beim adaptiven Filtern mit einer linearen Approximation des Gradienten der Zielfunktion, die zu folgenden dynamischen Anpassungsfunktionen führt: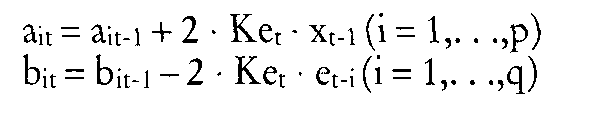
Adaptives Filtern

Dabei wird die Schnelligkeit der Anpassung über eine Lernkonstante K gesteuert, die im Bereich O < K < (l/(p + q)) liegen muß. Der Vorteil des adaptiven Filterns gegenüber dem Box-Jenkins-Verfahren liegt in dem erheblich verringerten mathematischen Aufwand und der leichteren Programmierbarkeit. Dem steht die geringere Genauigkeit und die Unsicherheit bei der Wahl der Lernkonstanten K gegenüber.

Literatur: Hansmann, K.-W., Kurzlehrbuch Prognoseverfahren, Wiesbaden 1983.
Literatur: Hüttner, M., Markt- und Absatzprognosen, Stuttgart u.a. 1982. Makridakis, S./Wheelwright, S. C., Interactive Forecasting, 2. Aufl., San Francisco 1978.

Vorhergehender Fachbegriff: Adaptive Selling | Nächster Fachbegriff: Adaptoren

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Kleingewerbetreibender | belastungsorientierte Auftragsfreigabe | ALF (Arbeitsgemeinschaft der Lebensmittel- Filialbetriebe e. V.)

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer