Hypothesenprüfung

Im Rahmen einer statistischen Hypothesenprüfung wird z. B. bezüglich eines Parameters einer Merkmalsverteilung über einer Grundgesamtheit eine Hypothese formuliert und anschliessend geprüft, ob diese aufgrund des Ergebnisses einer aus der Grundgesamtheit gezogenen Zufallsstichprobe verworfen werden muss oder nicht. Liegt z.B. über den Mittelwert i einer Merkmalsverteilung über der Grundgesamtheit eine Schätzung i₀ vor und liefert die Stichprobe einen Schätzwert x, so ist zu prüfen, ob das Stichprobenergebnis mit der Nullhypothese H₀ : i = i₀ verträglich ist oder ob ein statistisch signifikanter Unterschied zwischen |x und i₀ vorliegt (Alternativhypothese Hi : i =£ |i₀). Dabei kann es sich ergeben, dass aufgrund des Stichprobenergebnisses die Nullhypothese verworfen wird, obwohl sie wahr ist (Fehler 1. Art). Andererseits kann nicht ausgeschlossen werden, dass die Nullhypothese aufgrund des Stichprobenergebnisses nicht verworfen wird, obwohl sie nicht wahr ist (Fehler 2. Art). Beispiel: Das Durchschnittseinkommen |x₀ einer Grundgesamtheit von Personen werde mit jl₀ = 2200 DM pro Monat angenommen. Eine Überprüfung dieses Wertes bei einer Stichprobe im Umfang von n = 100 habe einen Wert von x = 2272 DM bei einer Standardabweichung von s = 300 ergeben. Es ist nun zu prüfen, ob das Stichprobenergebnis x innerhalb desjenigen Wertebereiches (Vertrauensbereiches) für x liegt, der bei Zugrundelegung einer Irrtumswahrscheinlichkeit von a = 5% (d.h. z_a = 1,96) für die Verträglichkeit mit der Nullhypothese H₀ : i = i₀ gilt. Liegt der Wert x ausserhalb des Vertrauensbereiches, so muss die Nullhypothese verworfen werden. Das Stichprobenergebnis stützt sie nicht. Andernfalls kann die Nullhypothese nicht verworfen werden, da das Stichprobenergebnis keine ausreichenden Anhaltspunkte dafür liefert. Es ergibt sich hier bei einem zweiseitigen Test folgendes Wahrscheinlichkeitsintervall: hypothesenprüfung

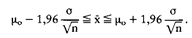Mit der Stichprobenstreuung bezüglich des Haushaltseinkommens von s = 300 als Schätzwert für die unbekannte Streuung der Grundgesamtheit o erhält man: 2142 DM = x ( 2258 DM. Da das Stichprobenergebnis x aber ausserhalb dieses Bereiches liegt, muss die Nullhypothese (|i = |i₀) bei einer Irrtumswahrscheinlichkeit von a = 5% verworfen werden. Eine Senkung der Irrtumswahrscheinlichkeit a führt stets zu einer Vergrösserung des Annahmebereiches und damit zu einer höheren Wahrscheinlichkeit eines Fehlers 2. Art. Es wurden eine Reihe von statistischen Testverfahren entwickelt, die entweder dazu dienen, Hypothesen über einen unbekannten Parameter der Grundgesamtheit, wie z. B. den Mittelwert, zu überprüfen ( Parametertest) oder wie bei einem sog. Chi-Quadrat-Test Hypothesen über die Verteilung der Grundgesamtheit zu testen ( Verteilungstest).

Der Ablauf statistischer Signifikanztests im Rahmen der Inferenzstatistik läßt sich grob in die Schritte Hypothesenformulierung, Festlegung des Signifikanzniveaus, Wahl einer geeigneten Testfunktion, Bestimmung des Verwerfungsbereichs und Entscheidungsfindung auf Basis der Realisation des Testfunktionswertes einteilen. Entscheidend ist die Einhaltung der Reihenfolge des Testablaufes. Insb. muss die Hypothesenformulierung vor der Analyse des vorliegenden Datenmaterials erfolgen (Bamberg/Baur (1989),S. 179). Man unterscheidet bei der Hypothesenformulierung hinsichtlich ihres Inhaltes zwei Grundtypen: Einerseits kann sich die Hypothese auf einen unbekannten Parameter beziehen, wie etwa auf den Lageparameter oder den Streuungsparameter der unbekannten Verteilung einer Grundgesamtheit. Man spricht bei Testverfahren dieses Hypothesentyps von parametrischen Tests. Andererseits kann sich die Hypothese auf die gesamte Gestalt der Verteilung des Untersuchungsmerkmals erstrecken. Es handelt sich dann um nichtparametrische oder verteilungsfreie Testverfahren. Bei der Hypothesenbildung werden meist zwei sich ausschließende Alternativen formuliert, nämlich die Nullhypothese Ho und die Gegen- oder Alternativhypothese Hi. Im letzten Schritt des Testablaufes, der Entscheidungsfindung, können nun zwei Fehlertypen auftreten. Einerseits kann die Nullhypothese verworfen werden, obwohl sie wahr ist (Fehler
1. Art), und andererseits kann die Nullhypothese angenommen werden, obwohl die Gegenhypothese wahr ist (Fehler
2. Art). Man versucht nun, die Hypothesen so zu formulieren, dass die maximale Wahrscheinlichkeit des möglichen Fehlers abgeschätzt werden kann. Zu diesem Zweck wird eine Nullhypothese gewählt, unter deren Gültigkeit die Verteilung der gewählten Testfunktion bekannt ist. Als Gegenhypothese formuliert man denjenigen Tatbestand, den man mit einer vorgegebenen zulässigen Fehlerwahrscheinlichkeit (dem Signifikanzniveau a) bestätigen will. Wird nun die Nullhypothese verworfen, da die Realisation der Testfunktion im Verwerfungsbereich liegt, wird zugleich die Gegenhypothese bestätigt und sichergestellt, dass die Wahrscheinlichkeit für den Fehler
1. Art kleiner gleich «liegt. Wird die Nullhypothese dagegen bestätigt, kann meist keine Aussage über die Wahrscheinlichkeit für einen Fehler
2. Art gemacht werden.

Vorhergehender Fachbegriff: Hypothesen-Matrix | Nächster Fachbegriff: Hypothesentest

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Inter-Mediaselection | Regiozentrischer Ansatz | Wertzoll

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer