| Empfehlungen |  |

Hysterese
|
(griechisch für: bleibend, zurückbleibend.) Ursprünglich innerhalb der Physik dazu verwendet, Bewegungsabläufe bei der Magnetisierung darzustellen. Ökonomische Anwendung erfährt die Hysterese in der Darstellung der Entwicklung der Arbeitslosigkeit. Auf dem Arbeitsmarkt bedeutet dies, dass die Arbeitslosigkeitsverläufe vor und nach einem exogenen Schock infolge der Zeitpfadabhängigkeit nicht auf gleichen Kurven erfolgen. Obwohl der die Arbeitslosigkeit verursachende Schock nicht mehr existiert, ist die Arbeitslosigkeit auf einen höheren Gleichgewichtswert eingeschwenkt, d. h. sie sinkt nicht mehr auf das Niveau vor dem Schock ab. Empirisch wird Hysterese in dem treppenförmigen Anstieg der Arbeitslosigkeit nach jedem Konjunktureinbruch in den letzten 26 Jahren sichtbar. beschreibt eine bestimmte Eigenschaft eines dynamischen Systems im Hinblick auf seinen langfristigen Gleichgewichtswert (steady state). Dieser Gleichgewichtswert wird bei Vorliegen von Hysterese nicht nur von den gleichgewichtigen Werten der dieses System bestimmenden exogenen Variablen determiniert, sondern darüber hinaus auch von den Anfangsbedingungen der Zustandsvariablen und von den Werten der exogenen Variablen auf dem Zeitpfad hin zum Gleichgewicht. Dynamische Systeme mit Hysterese sind deshalb zeitpfadabhängige Systeme. Das Konzept der Hysterese wurde übernommen aus der Physik resp. der sog. Hyste- resis-Schleife, die den Verlauf der magnetischen Induktion eines ferromagnetischen Materials infolge eines angelegten Magnetfeldes mit stetig steigender und dann sinkender Feldstärke kennzeichnet. Besondere Bedeutung hat dieses Konzept im Rahmen der Erklärung anhaltend hoher Arbeitslosigkeit und der Effizienz von Arbeitsmarktpolitik erlangt. Die übliche erweiterte Phillips-Kurve ist dargestellt durch 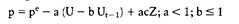 (mit: p resp. pe aktuelle resp. erwartete Inflationsrate; U resp. Ut_i Arbeitslosenquote dieser resp. der vorhergehenden Periode; Z exogene Schock- bzw. Bestimmungsgrössen; [a, b, e] exogene, konstante, positive Koeffizienten). Setzt man zur Bestimmung der inflationsstabilen Arbeitslosenquote (NAIRU) NU: p = pe - a (U - NU), so folgt aus beiden Gleichungen die Bestimmung von NU: (mit: p resp. pe aktuelle resp. erwartete Inflationsrate; U resp. Ut_i Arbeitslosenquote dieser resp. der vorhergehenden Periode; Z exogene Schock- bzw. Bestimmungsgrössen; [a, b, e] exogene, konstante, positive Koeffizienten). Setzt man zur Bestimmung der inflationsstabilen Arbeitslosenquote (NAIRU) NU: p = pe - a (U - NU), so folgt aus beiden Gleichungen die Bestimmung von NU: 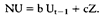 Für b = 0 gibt es jeweils einen eindeutigen, nur von den exogenen Grössen Z abhängigen Wert der NAIRU. Für 0 < b < 1 hängt der Wert der NAIRU von der Arbeitslosenquote der Vorperiode ab, so dass sich der Wert der NAIRU von Periode zu Periode ändert ( Persistenz); der langfristige Wert E(NU) im (steady-state; U = Ut_i = .. NU) Gleichgewicht ist dann vom langfristigen Wert der exogenen Grössen E(Z) und dem Parameter b abhängig: Für b = 0 gibt es jeweils einen eindeutigen, nur von den exogenen Grössen Z abhängigen Wert der NAIRU. Für 0 < b < 1 hängt der Wert der NAIRU von der Arbeitslosenquote der Vorperiode ab, so dass sich der Wert der NAIRU von Periode zu Periode ändert ( Persistenz); der langfristige Wert E(NU) im (steady-state; U = Ut_i = .. NU) Gleichgewicht ist dann vom langfristigen Wert der exogenen Grössen E(Z) und dem Parameter b abhängig: 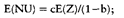 b bestimmt den Zeitpfad der Annäherung an den Gleichgewichtswert. Für b = 1 gibt es keine eindeutige Gleichgewichtslösung der NAIRU (da allgemein ausgedrückt die Übergangsmatrix des dynamischen Gleichungssystems singulär ist). Es gibt unendlich viele Ausprägungen, wobei die Bestimmung des eintretenden Wertes die Kenntnis der Ausgangssituation und des Entwicklungspfades der Arbeitslosenquote voraussetzt ( Simulation). Der Gleichgewichtswert ist damit pfadabhängig; die inflationsstabile Arbeitslosenquote variiert pari passu mit der tatsächlich realisierten. Die Rückkehr zum alten steady-state-Wert der NAIRU nach einem exogenen Schock ist nicht für jede Art von Schock prinzipiell ausgeschlossen (Hysterese bedeutet nicht Irreversibilität), sie setzt aber einen gleichstarken entgegengesetzten Schock voraus. Damit erscheint in einigen Fällen eine den Wirtschaftsprozess beeinflussende diskretionäre Wirtschaftspolitik sinnvoll und möglich. Die bekanntesten Erklärungsansätze für Persistenz und Hysteresis-Effekte auf dem Arbeitsmarkt sind die sog. Insider-Outsider-Theorie, das Kapital-Knappheitsargu- ment, die Dezelerationshypothese und die Dequalifizierungshypothese infolge von Lang- zeitarbeitslosigkeit bei Humankapitalverlust oder bei Diskriminierung. Die wirtschaftspolitische Implikation des Hysterese-Phänomens liegt darin, dass sich ein Gleichgewichtswert, der sich deshalb neu eingestellt hat, weil bestimmte Faktoren an Bedeutung gewonnen haben, auch dann nicht oder nur allmählich (zurück)verändert, wenn diese Faktoren nicht mehr relevant sind. So hat z.B. die erhebliche Reduktion der Erdölpreise in der jüngeren Vergangenheit nicht dazu geführt, dass sich die Arbeitslosigkeit in der Bundesrepublik Deutschland in dem Masse zurückgebildet hat, wie sie - ausgelöst durch den exorbitanten Anstieg dieser Preise 1974 und 1979 - zugenommen hat. Literatur: Franz, W, Das Hysteresis-Phänomen, in: WiSt, 18. Jg. (1989), S. 77ff. Layard, RJCalmfors, L. (Hrsg.), The Fight against Unemployment, Cambridge, Mass. 1987. Cross, RJ Allan, A., On the History of Hysteresis, in: Cross, R. (Hrsg.), Unemployment, Hysteresis and the Natural Rate Hypothesis, Oxford 1988, S. 26 ff.. b bestimmt den Zeitpfad der Annäherung an den Gleichgewichtswert. Für b = 1 gibt es keine eindeutige Gleichgewichtslösung der NAIRU (da allgemein ausgedrückt die Übergangsmatrix des dynamischen Gleichungssystems singulär ist). Es gibt unendlich viele Ausprägungen, wobei die Bestimmung des eintretenden Wertes die Kenntnis der Ausgangssituation und des Entwicklungspfades der Arbeitslosenquote voraussetzt ( Simulation). Der Gleichgewichtswert ist damit pfadabhängig; die inflationsstabile Arbeitslosenquote variiert pari passu mit der tatsächlich realisierten. Die Rückkehr zum alten steady-state-Wert der NAIRU nach einem exogenen Schock ist nicht für jede Art von Schock prinzipiell ausgeschlossen (Hysterese bedeutet nicht Irreversibilität), sie setzt aber einen gleichstarken entgegengesetzten Schock voraus. Damit erscheint in einigen Fällen eine den Wirtschaftsprozess beeinflussende diskretionäre Wirtschaftspolitik sinnvoll und möglich. Die bekanntesten Erklärungsansätze für Persistenz und Hysteresis-Effekte auf dem Arbeitsmarkt sind die sog. Insider-Outsider-Theorie, das Kapital-Knappheitsargu- ment, die Dezelerationshypothese und die Dequalifizierungshypothese infolge von Lang- zeitarbeitslosigkeit bei Humankapitalverlust oder bei Diskriminierung. Die wirtschaftspolitische Implikation des Hysterese-Phänomens liegt darin, dass sich ein Gleichgewichtswert, der sich deshalb neu eingestellt hat, weil bestimmte Faktoren an Bedeutung gewonnen haben, auch dann nicht oder nur allmählich (zurück)verändert, wenn diese Faktoren nicht mehr relevant sind. So hat z.B. die erhebliche Reduktion der Erdölpreise in der jüngeren Vergangenheit nicht dazu geführt, dass sich die Arbeitslosigkeit in der Bundesrepublik Deutschland in dem Masse zurückgebildet hat, wie sie - ausgelöst durch den exorbitanten Anstieg dieser Preise 1974 und 1979 - zugenommen hat. Literatur: Franz, W, Das Hysteresis-Phänomen, in: WiSt, 18. Jg. (1989), S. 77ff. Layard, RJCalmfors, L. (Hrsg.), The Fight against Unemployment, Cambridge, Mass. 1987. Cross, RJ Allan, A., On the History of Hysteresis, in: Cross, R. (Hrsg.), Unemployment, Hysteresis and the Natural Rate Hypothesis, Oxford 1988, S. 26 ff..
Vorhergehender Fachbegriff: Hypothetisches Konstrukt | Nächster Fachbegriff: HZA Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken |
|
Schreiben Sie sich in unseren kostenlosen Newsletter ein
Bleiben Sie auf dem Laufenden über Neuigkeiten und Aktualisierungen bei unserem Wirtschaftslexikon, indem Sie unseren monatlichen Newsletter empfangen. Garantiert keine Werbung. Jederzeit mit einem Klick abbestellbar.
Weitere Begriffe : Kreuzpreiselastizitätskoeffizient | Pfaddiagramm | Box
|
Praxisnahe Definitionen Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar. |
Fachbegriffe der Volkswirtschaft Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre. |
Beliebte Artikel Bestimmte Erklärungen und Begriffsdefinitionen erfreuen sich bei unseren Lesern ganz besonderer Beliebtheit. Diese werden mehrmals pro Jahr aktualisiert. |
