Minimax-Regret-Regel

(Savage-Niehans-Regel, Regel des geringsten Bedauerns): Eine von L. J. Savage in der Entscheidungstheorie
entwickelte Regel für Entscheidungen unter Unsicherheit (verteilungsfreier Fall), die der Maximin-Regel sehr verwandt ist. Ebenso wie das Maximin-Kriterium ist die Ausgangsposition eine pessimistische Grundhaltung. Vom Entscheider wird erwartet, dass er sich für diejenige Handlungsalternative entscheidet, bei der das maximale Bedauern pro Alternative minimiert wird. Er soll also diejenige Strategie wählen, bei der bei Eintreten eines bestimmten Umweltzustandes das Ausmass der Frustration oder Enttäuschung des Entscheidungsträgers
darüber, dass er nicht die nun eindeutig bestimmbare optimale Strategie gewählt hat, so gering wie möglich ist. Der Entscheidungsträger wählt mithin diejenige Strategie, bei der er sicher gehen kann, weniger als bei jeder anderen Strategie zu verlieren, d.h. weniger als in allen anderen alternativen Strategieoptionen enttäuscht zu sein.
Für jede Konsequenz o; kann ein Bedauerns-Wert (regret) berechnet werden; er ergibt sich als die Differenz zwischen der bei gegebenen bi maximal möglichen Auszahlung und der bei alb faktisch sich ergebenden Auszahlung. Die folgende Tabelle zeigt eine Auszahlungsmatrix und die ihr entsprechende Matrix der Bedauerns-Werte:
Den Bedauerns-Wert für Konsequenz 011 erhält Bedauernsmatrix man, indem man die Auszahlung bei a1b1 von der bei gegebenen b1 maximal möglichen Auszahlung subtrahiert.

Diese Größe wird als “Bedauerns-Wert” bezeichnet, weil PA ja bedauern würde, nicht Strategie a3 gewählt zu haben, wenn er feststellen muss, dass PB die Strategie b1 gewählt hat; denn mit a3 hätte er unter dieser Bedingung die maximal mögliche Auszahlung erzielt. Das Ausmass des Bedauerns von PA hängt von der Größe der Differenz zwischen der faktischen Auszahlung aufgrund seiner Entscheidung und derjenigen Auszahlung ab, die er hätte erhalten können. Wenn PA ohnehin die Alternative wählt, bei der die Auszahlung bei gegebenem bi maximal ist, kann sein Bedauerns-Wert für die entsprechende Konsequenz nur 0 sein. Definitionsgemäss muss somit mindestens eine Zelle in jeder Spalte der Bedauerns-Matrix 0 sein und müssen die restlichen Zellen positive Werte enthalten; für PB sind die Bedauerns-Werte natürlich auf die Strategien a;, also die Zeilen der Bedauerns-Matrix bezogen, so dass jede Zeile zumindest einen Bedauerns-Wert von 0 enthält.
Nach dem Minimax-Regret-Prinzip sollte PA die Alternative mit dem minimalen der maximalen Bedauerns-Werte wählen. Bei jeder reinen Strategie a; gibt es einen maximalen - bzw. bei gemischten Strategien einen erwarteten - Bedauerns-Wert, und PA sollte sich für die Strategie mit dem geringsten dieser Maxima entscheiden. Die Lösung findet man, indem man die Werte der Bedauerns-Matrix mit negativem vorzeichen versieht, diese Werte dann als “Auszahlungen” interpretiert und die Maximin-Lösung berechnet.

Auszahlungsmatrix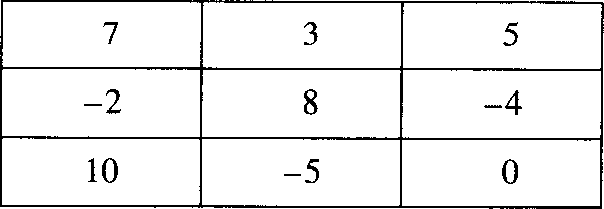

Minimax-Regret-Regel

Vorhergehender Fachbegriff: Minimax-Regel | Nächster Fachbegriff: Minimax-Risiko-Regel

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Zuverlässigkeitstheorie | Grundkreditanstalten | Lernkurve

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer