Autokorrelation

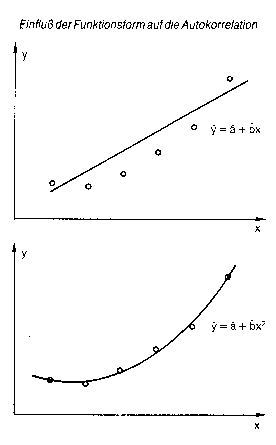bedeutet, dass die Störvariablen bei gegebenen erklärenden Variablen x_lt, ..., x_nt in einem Regressionsmodell intertemporal korreliert sind, d.h. E(u_tu_t./x_lt,..x_nt) + 0 Als wichtige Ursachen autokorrelierter Störvariablen sind zu nennen: • Vernachlässigung wichtiger erklärender Variablen: Ökonometrische Zeitreihen sind ort autokorreliert; denn die Werte der Periode t hängen im allgemeinen stark von den Werten der Periode t-1 ab. Liegt eine solche trendmässige Entwicklung vor, so ist davon auszugehen, dass auch solche Variablen autokorreliert sind, die nicht im Modellansatz berücksichtigt wurden. Diese autokorrelierten Variablen werden durch u mitrepräsentiert, dessen Werte dann ebenfalls autokorreliert sind. Dieser Effekt ist allerdings nicht leicht zu zeigen, da Kompensationseffekte unvermeidlich sind. • Wahl einer falschen Funktionsform: Die Werte der Störvariablen u_t werden als Differenz zwischen Funktionswert y und realisiertem Wert y ermittelt. Der Funktionswert kann aber durch die Wahl eines anderen mathematischen Grundansatzes verändert werden (vgl. Abb.). Verwendung saisonbereinigter Werte: Werden in ökonometrischen Modellen saisonbereinigte Werte verwendet, dann besteht die Gefahr, dass der Glättungsalgorithmus, der die Zufallsschwankungen auf mehrere, zeitlich aufeinanderfolgende Werte verteilt, Abhängigkeiten zwischen den Werten erzeugt. Literatur: Hujer, RJCremer, R., Methoden der empirischen Wirtschaftsforschung, München 1978. Hübler; 0., Ökonometrie, Stuttgart, New York 1989.

siehe Ökonometrie (mit Literaturangaben).

Problem bei der Analyse von Zeitreihen mit der linearen Regressionsanalyse. Es tritt auf, wenn die Annahme unkorrelierter Residuen verletzt ist mit der Folge (Autokorrelation
1. Ordnung), dass 1) E(£t,£t-l) * 0

und es gilt 2) £t = p £t-i + ut (für alle t),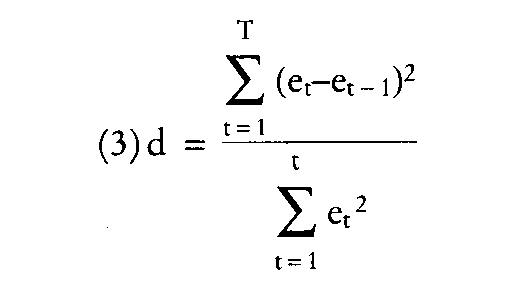
Autokorrelation

mit dem Parameter p < 1 und ut ist eine normalverteilte Zufallsvariable. Obwohl die Schätzer des Regressionsmodells b unverzerrt (unbiased) sind, wird die Kleinste- Quadrate-Methode die Stichprobenvarianzen unterschätzen. Die Folge davon ist, dass die t-Tests die Regressionskoeffizienten im Modell eher überbewerten. Eine statistische Prozedur zur Identifikation von Autokorrelation lieferten Durbin & Watson mit der Teststatistik. Die Statistik wird aus den Residuen der Kleinsten Quadrate-Schätzung berechnet. Der Test liefert keine exakte Signifikanzschwelle für d, sondern eine untere und eine obere Schranke di. und du unter Berücksichtigung der Anzahl der Beobachtungen und der Anzahl der unabhängigen Variablen in der Regressionsgleichung. Die Entschei- dungsregeln bei Annahme positiver Autokorrelation (Alternativhypothese: Ha : p > 0) sind dann
1. d<dL pos. Autokorrelation
2. dL < d < du ohne Aussage
3. d > du keine positive Autokorre lation. Bei positiver oder negativer Autokorrelation sind die Entscheidungsregeln
1. d < dLoderd > 4-di. Autokorrelation
2. du < d < 4-du keine Autokor relation
3. dL < d < du oder 4-du < d < 4-dL ohne Aussage. Oft genügt zur Analyse der Autokorrelation das Scattergramm der Störterme. Eine Möglichkeit der Beseitigung der Autokorrelation besteht in der Differenzenbildung der Werte derZeitreihe.

Literatur: Kmenta,}., Elements of Econometrics, 2. Aufl.,NewYork 1986.

Abhängigkeit einer Variablen von sich selbst. Meist wird dieser Begriff jedoch nur auf Störgrößen in Regressionsmodellen mit Zeitreihendaten angewandt. Gründe für Autokorrelation können sein: temporale Aggregation von individuellen Störgrößen, die selbst unkorreliert sind, unterdrückte Variablen oder ein falsch angenommener Funktionsverlauf. Unterschieden wird zwischen Autokorrelation erster und höherer Ordnung sowie zwischen negativer und positiver Autokorrelation. Die Existenz von Autokorrelation hat zur Konsequenz, dass Schätzungen nach der gewöhnlichen Methode der kleinsten Quadrate ineffizient sind, dass sich falsche Standardfehler ergeben. Ob Autokorrelation vorliegt, kann durch Tests geprüft werden. Auf Autokorrelation erster Ordnung wird üblicherweise mit Hilfe des DURBIN-WATSON-Tests geprüft. Wird die Nullhypothese (keine Autokorrelation) abgelehnt, so bietet sich als Schätzung ein zweistufiges bzw. iteratives EGLS-Verfahren an, wonach zunächst der Autokorrelationskoeffizient zu schätzen ist, um dann unter Berücksichtigung dieses Wertes die Variablen zu transformieren und mit Hilfe der OLS-Methode die Koeffizienten aus dem transformierten Modell zu schätzen. Der DURBIN-WATSON-Test ist ungeeignet, wenn Autokorrelation höherer Ordnung vorliegt und verzögerte endogene Variablen auftreten. Ausgehend von einem Ansatz mit dem Residuum als Regressand sowie verzögerten Residuen und den exogenen Variablen des Ausgangsmodells als Regressoren, kann in diesem Fall auf Autokorrelation getestet werden. Literatur: Hübler, O. (1989). Judge, G.G. u.a. (1985). Johnston, J. (1984)

Vorhergehender Fachbegriff: Autographen | Nächster Fachbegriff: Autokorrelations-Test

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Horizontaler Spread | Importdruck | IBCC

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer