Dualität und Dualitätstheorie

Zu jedem (primalen) LP-Modell lässt sich auf systematische Weise ein duales LP-Modell konstruieren. Es lässt sich beweisen (Einschließungssatz), dass primales und duales Modell denselben optimalen Zielfunktionswert haben. Außerdem gibt es enge Beziehungen zwischen den jeweiligen optimalen Lösungen (z.B. Satz vom komplementären Schlupf), die simultan durch den Simplex-Algorithmus ermittelt werden. Die Dualitätsbeziehung wird daher häufig in Lösungsverfahren ausgenutzt (z.B. MODI-Methode). Für das primale Modell P in Maximierungsform ergibt sich das duale Modell D: Minimiere FD(w) = bTw (D) NB: ATw c, w 0 Anschaulich entspricht die Dualisierung einer Spiegelung des Problems: Nebenbedingungs- werden zu Zielfunktionskoeffizienten und umgekehrt, die Anzahl der Nebenbedingungen in P bestimmt die Anzahl der Variablen in D und umgekehrt, Maximierung wird zu Minimierung, -Bedingungen werden zu -Bedingungen.

Die Dualität ist ein Begriff aus der linearen Programmierung. Jedes lineare Problem kann in ein duales Problem überführt werden, das das gleiche Ergebnis liefert. Das duale Problem ergibt sich aus der Inversion der Koeffizientenmatrix. Soll beim originären Problem (Primal) eine Gewinnmaximierung d.er Produktmengen erzielt werden, so läßt sich dasselbe Ziel durch das dazugehörige Dual über die Minimierung der Kosten erreichen. Damit wird ein gewinnmaximales Primal in ein kostenminimales Dual transponiert. Im kostenminimalen Dual wird jedoch nicht mit realen Faktorpreisen, sondern mit Opportunitätskosten gerechnet.

(= Zweiheit, Vertauschbarkeit) bezeichnet die Möglichkeit, ökonomische Strukturzusammenhänge mit zwei unterschiedlichen Konzepten gleichwertig zu beschreiben. Beispiele sind:
1. Produktionstheorie: Sind die Produktionsbedingungen z.B. eines Unternehmens durch eine Produktionsfunktion beschreibbar, dann können sie auch durch eine Kostenfunktion beschrieben werden. Zu einer Produktionsfunktion gehört eine bestimmte Kostenfunktion und umgekehrt. So korrespondiert mit der linearhomogenen COBB-DOUGLAS-Produktionsfunktion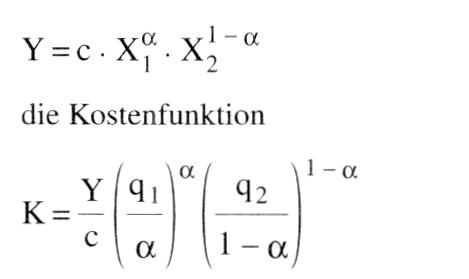
Dualität

wobei q1 und q2 die Preise der Einsatzfaktoren X1 und X2 sind und c > 0,0 < a < 1 Parameter darstellen.
2. Nutzentheorie: Die Präferenzen eines Individuums können durch eine direkte Nutzenfunktion (Nutzenindex in Abhängigkeit von Güterquantitäten) oder eine indirekte Nutzenfunktion beschrieben werden (maximal erreichbarer Nutzenindex in Abhängigkeit vom Einkommen und den relevanten Güterpreisen). Die Eigenschaften beider Funktionen bedingen einander.
3. Lineare Programmierung: Möglichkeit der Überführung eines Maximierungsproblems in ein Minimierungsproblem und umgekehrt. Dualität erleichtert die Aufdeckung und Quantifizierung ökonomischer Strukturzusammenhänge. So können die Produktionsbedingungen eines Unternehmens häufig einfacher mittels der Kostenfunktion erschlossen werden, weil Informationen über Kosten und Preise eher zu erlangen sind als Informationen über Faktoreinsatzmengen. Literatur: Varian, H.R. (1992)

Vorhergehender Fachbegriff: Dualität | Nächster Fachbegriff: Dualsystem

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Institute War Clauses (Cargo) | Innovationsorganisation | VL-sparvertrag

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer