Erwartungswert

Nach Sieben und Schildbach ist der mathematische Erwartungswert definiert als die Summe über alle Umweltsituationen der mit den Eintrittswahrscheinlichkeiten pj gewichteten Zielerreichungsgrade.

In der Wirtschaftssoziologie: der theoretische Mittelwert einer Wahrscheinlichkeitsverteilung; für diskrete Verteilungen die Summe aller Produkte aus möglichen Werten und zugehöriger Wahrscheinlichkeit. Der Erwartungswert ist der Wert, den man bei genügend grossem Stichprobenumfang im Durchschnitt erwarten kann (Gesetz der grossen Zahlen).

Der Erwartungswert E(X) einer diskreten Zufallsvariablen X mit den Ausprägungen Xj (i = 1,2,...) und der Wahrscheinlichkeitsfunktion (Zufallsvariable) ffo) (i = 1, 2.. ..) ist defini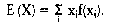ert als

Für eine stetige Zufallsvariable X mit der Dichtefunktion f(x) (Zufallsvariable) ist der Erwartungswert definiert als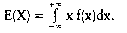

Der Erwartungswert ist also das arithmetische Mittel der Zufallsvariablen X. Der Erwartungswert kann auch für Zufallsvariablen, die als Funktion einer oder mehrerer Zufallsvariablen definiert sind, bestimmt werden. So ist der Erwartungswert der Funktion [X - E(X)]² identisch mit der Varianz Var(X); es gilt also Var(X) = E[[X-E(X)]²]. Für eine diskrete Zufallsvariable X gilt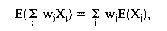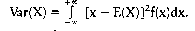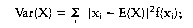

ist eine Zufallsvariable X stetig, so gilt Für den Erwartungswert einer Linearkombination von Zufallsvariablen Xj (j = 1, 2.. .., p) erhält man: wobei die Koeffizienten Wj (j = 1, 2, ..., p) beliebige reelle Zahlen sind. Literatur: Bleymüller, J.lGehlert, G./Gülicher, H., Statistik für Wirtschaftswissenschaftler, 8. Aufl., München 1992.

bezeichnet die durchschnittlich zu erwartende Realisation einer Zufallsvariablen. Bei Vorliegen einer diskreten Wahrscheinlichkeitsverteilung einer Zufallsvariablen ergibt sich der Erwartungswert als der mit den jeweiligen Eintrittswahrscheinlichkeiten gewichtete Durchschnitt der denkbaren Ergebnisse der Zufallsvariablen.

In der statistischen Schätztheorie ein zur Ermittlung der Erwartungstreue einer Schätzfunktion verwendeter Wert, der aus dem Mittelwert der Grundgesamtheit besteht, der bei mehrfacher Zufallsentnahme für die Zufallsgröße X zu erwarten ist. Für den diskreten Fall gilt also, wenn x; (1 <_ i <_ k) die Ausprägungen der Zufallsgröße X und 1(9 die zugehörigen Wahrscheinlichkeiten bezeichnen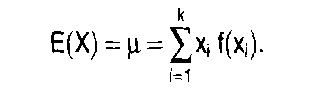

Dabei ergibt sich der systematische Fehler (Bias) als die Differenz zwischen Erwartungswert und Parameter. Umgekehrt ist eine Schätzung erwartungstreu, wenn Erwartungswert und wahrer Wert gleich sind.

Vorhergehender Fachbegriff: Erwartungstreue | Nächster Fachbegriff: Erwartungswert-Maxime

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Cross Currency Basis Swap | Ec | Kostenprogression

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer