Investitions-Finanzierungs-Modelle

Modelle zur Bestimmung des optimalen Investitionsprogramms und des optimalen Finanzierungsprogramms bei sicheren Erwartungen enthalten neben Investitionsvariabler auch Finanzierungsvariablen. Inwieweit vor den durch Finanzierungsvariablen repräsentierten Finanzierungsmöglichkeiten Gebrauch gemacht wird, hängt u.a. von den bestehenden Investitionsmöglichkeiten ab (und umgekehrt). Die Optimierung von Investitionsund Finanzierungsprogramm sollte deshalb simultan erfolgen. Die Struktur eines Investitions-Finanzierungs-Modells wird im folgenden anhand des Mehrperiodenmodells von Herbert Hax und H. M. Weingartner erläutert: Gesucht sind die Investitions- und Finanzierungsprogramme für die Teilperioden t = 1, ..., T, die den Vermögensendwert maximieren. Dabei sind Nebenbedingungen z.B. zur Sicherung der Zahlungsfähigkeit und hinsichtlich der Kre- ditvolumina zu beachten. Zielfunktion: investitions finanzierungs modelle

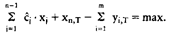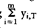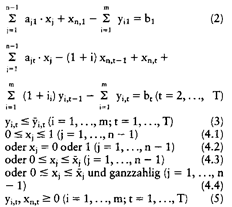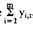Der obige Ausdruck repräsentiert den Vermögensendwert. Er ergibt sich als Summe der auf den Planungshorizont T diskontierten Zahlungen der Investitionsprojekte Xj (j = 1, ..., n - 1), soweit sie jenseits des Planungshorizonts anfallen (t T), und der Differenz aus dem Geldvermögensbestand x_nT und der Verschuldungim Planungshorizont. Nebenbedingungen : investitions finanzierungs modelle

Die Nebenbedingungen (2) stellen für alle Perioden t = 1,..., T das finanzielle Gleichgewicht sicher. Sofern in einer Periode ein Finanzmittelüberschuss entsteht, wird dieser für ein Jahr verzinslich angelegt (x_njt). Wenn sich hingegen in einer Periode eine Finanzmittelunterdeckung ergibt, so wird die Finanzierungslücke durch Aufnahme von Krediten in der Höhe, rückzahlbar nach einem Jahr, gedeckt. Die Nebenbedingungen (3) gewährleisten, dass die Kredithöchstbeträge der einzelnen Finanzierungsarten eingehalten werden. Die alternativ formulierten Nebenbedingungen (4) stellen Beschränkungen für die Realinvesti- tionsprojekte dar. Kann höchstens eine Einheit eines Projekts realisiert werden, so ist die Bedingung (4.2) oder aus Gründen der rechnerischen Vereinfachung unter Aufgabe der Ganzzahligkeit die Bedingung (4.1) zu wählen. Können höchstens Xj 1 Einheiten eines Projekts realisiert werden, so ist die Bedingung (4.4) oder aus Gründen der rechentechnischen Vereinfachung unter Aufgabe der Ganzzahligkeit die Bedingung (4.3) zu wählen. Literatur: Blohm, H.ILüder, K., Investition, 7. Aufl., München 1991, S. 284 ff. Lüder, K. (Hrsg.), Investitionsplanung, München 1977, S. 243 ff.

Vorhergehender Fachbegriff: Investitions-Controlling | Nächster Fachbegriff: Investitions-Produktions-Modelle

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Lagern | öGmbHG | Short Put

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer