Kovarianz

Die Kovarianz ist ein Begriff aus der Statistik und steht für den (abweichenden) Unterschied bei zwei Reihen von Messwerten.

Die Kovarianz ist das gemittelte Produkt der Abweichungs-Wertpaare.

In der Wirtschaftssoziologie: Ausdruck für das gemeinsame Variieren zweier Variablen um ihre Mittelwerte. Die Kovarianz ist definiert als die Summe der Produkte der Abweichungen der Messwertpaare (x,; yi) von ihren Mittelwerten (x; y) dividiert durch N: (xt - x) (y; - y) N ist die Zahl der untersuchten Einheiten, an denen die Variablen x und y gemessen werden. Streuen die Variablen unabhängig voneinander um ihre Mittelwerte, so ist die Kovarianz gleich null. Die Kovarianz geht in den Pearsonschen Produkt-Moment-Korrelationskoeffizienten ein. Kovarianzanalyse, Untersuchung der Beziehungen zwischen den Kovarianzen in einer Menge von drei oder mehr Variablen. Mit Kovarianz wird i.d.R. der Fall bezeichnet, in dem Intervallskalen und Nominalskalen gemeinsam untersucht werden, etwa in Form der Zerlegung der Kovarianz zweier Intervallskalen nach den Kategorien einer Nominalskala. Obwohl die Kovarianz für soziologische Fragestellungen besondere Bedeutung besitzen dürfte, wird sie nur selten durchgeführt.

Mass für die Stärke des Zusammenhanges zwischen zwei Variablen. Im Gegensatz zum Korrelationskoeffizienten (Korrelationsanalyse) hängt der numerische Wert der Kovarianz von den bei der Messung der Variablen zugrundegelegten Masseinheiten ab. Sind X und Y zwei Zufallsvariablen, dann ist die Kovarianz Cov(X,Y) der Erwartungswert der Funktion [X-E(X)] • [Y-E(Y)], also Cov(X,Y) = E [X-E(X)] • [Y-E(Y)]. Sind X und Y unabhängig, dann ist ihre Kovarianz Null. Liegen für zwei Variablen X und Y n Stich- probenwertepaare (Xj,yj) (i = 1, ..., n) vor, dann ist die Stichprobenkovarianz Sxy ^zwi^_ sehen diesen Variablen als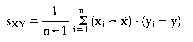

definiert, wobei x und y die Stichprobenmittelwerte der beiden Variablen sind (arithmetisches Mittel); es gilt also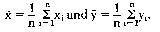

Zwischen der Stichprobenkovarianz und dem entsprechenden Korrelationskoeffizienten rxy besteht die Beziehung sxy = s_x • s_Y • r_XY, wobei s_x bzw. s_Y die Standardabweichung von X bzw. Y bezeichnet. Literatur: Bleymüller, J./Gehlert, GJGülicher, H., Statistik für Wirtschaftswissenschaftler, 8. Aufl., München 1992. Flury, BJRiedwyl, H., Multivariate Statistics - A Practical Approach, London u. a. 1988.

Vorhergehender Fachbegriff: Koupon | Nächster Fachbegriff: Kovarianzanalyse

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Fixkostenmanagement | E-Sourcing | Matrixorganisation

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer