Sattelpunkt-Lösung

liegt bei einem Zwei-Personen-Nullsummenspiel (Spieltheorie) ohne gemischte Strategien (Handlungsalternative) immer dann vor, wenn bei Befolgung des Mini-MaxPrinzips durch beide Spieler das maximale Gewinnminimum und das minimale Verlustmaximum übereinstimmen. Beispiel 1: Zwei Spielern A und B stehen die Strategien a_b a₂, a₃ bzw. b₁, b₂, b₃ zur Auswahl, die zu dem in folgender Spielmatrix jeweils angegebenen Gewinn für A (= Verlust für B) führen: Richten sich beide Spieler bei der Auswahl ihrer Strategien nach dem Mini-Max-Prinzip, so realisiert A die Strategie a₃, die das maximale Gewinnminimum aufweist, und B die Strategie b₂ mit dem minimalen Verlustmaximum. Stimmen maximales Gewinnminimum und minimales Verlustmaximum überein, so bildet der durch das entsprechende Strategien-paar gekennzeichnete Ergebniswert in der Spielmatrix einen Sattelpunkt. 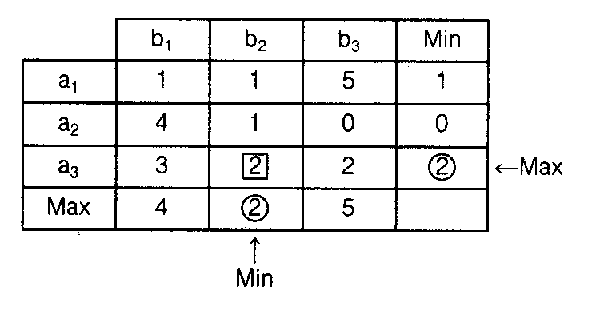Die Sattelpunkt-Lösung hat dabei folgende Gleichgewichtseigenschaften: · Glaubt ein Spieler, der andere werde sich gemäss dem Mini-Max-Prinzip verhalten, so ist es für ihn selbst optimal, ebenfalls dem Mini-Max-Prinzip zu folgen. · Wählen beide Spieler die entsprechenden Strategien, so stimmt das tatsächlich eintretende Ergebnis für jeden mit dem erwarteten überein. Es spricht vieles dafür, dass sich in einer derartigen Spielsituation auch tatsächlich die Sattelpunkt-Lösung einstellen wird, sofern beide

Spieler die Situation richtig erkennen und sich rational verhalten. Zugleich erscheint es sinnvoll, jedem einzelnen Spieler in solchen Situationen die Befolgung des Mini-Max-Prinzips als vernünftige Verhaltensweise zu empfehlen. Der Gültigkeitsbereich der Sattelpunkt-Lösung bei Spielen ohne gemischte Strategien ist allerdings begrenzt, da viele Spiele überhaupt keine solche Lösung aufweisen. Beispiel 2: Gegenüber dem Beispiel 1 wird nur das Ergebnis der Strategienkombination a₁/b₂ geändert. Die Mini-Max-Strategien a₃/b₂ bilden nun keine Sattelpunkt-Lösung mehr. Geht A z. B. davon aus, dass B b₂ realisiert, so wäre es für ihn optimal, a_l — und nicht die Mini-Max-Strategie a₃ — zu realisieren. Antizipiert B die entsprechende Absicht von A, so wäre es für ihn am besten, b₁ zu wählen. Ahnt A dieses wiederum, so würde er auf a₂ übergehen, etc. Sind in einem Zwei-Personen-NullsummenSpiel auch gemischte Strategien zugelassen, so kann allerdings stets eine Sattelpunkt-Lösung mit den zuvor angegebenen Gleichgewichtseigenschaften gefunden werden, sofern beide Spieler die mit der Wahl einer gemischten Strategie verbundenen unsicheren Ergebniswerte durch den jeweiligen mathematischen Erwartungswert zu einem Wert zusammenfassen. Beispiel 3: In Erweiterung von Beispiel 2 sind in folgender Spielmatrix für A und B jeweils zusätzlich zwei gemischte Strategien vermerkt, nämlich · zum einen als a₄ (b₄) die Möglichkeit, alle drei "reinen" Strategien mit einer Wahrscheinlichkeit von 1/2 einzusetzen, · zum anderen als a₅ (b₅) die Möglichkeit, a_l (b₁) mit 1/2-Wahrscheinlichkeit sowie a₃ (b₂) mit ²/3-Wahrscheinlichkeit einzusetzen und auf a₂ (b₃) ganz zu verzichten. Berechnet man für diese Strategien jeweils die Erwartungswerte, so ergibt sich folgende Spielmatrix, in der die gemischten Strategien a_s/b₅ wiederum eine Sattelpunkt-Lösung darstellen (vgl. nachstehende Abb.). Die Ermittlung der einer Sattelpunkt-Lösung entsprechenden gemischten Strategien ist allgemein mit Hilfe der —linearen Optimierung, in einfachen Fällen auch mittels grafischer Methoden möglich.

Vorhergehender Fachbegriff: Sattelpunkt | Nächster Fachbegriff: Sattelpunktstrategien

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Datenwürfel | Verbrauchsgut | Kommerzialrat

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer