WALRASsches Gesetz

nach Leon WALRAS (1834-1910) benanntes Gesetz, das sich insbes. auf das Modell des allgemeinen kompetitiven Gleichgewichts bezieht und besagt, dass bei beliebigen Preisen die über alle Märkte und Wirtschaftssubjekte aggregierte wertmäßige Nachfrage dem aggregierten wertmäßigen Angebot gleich ist. Das WALRASsche Gesetz ergibt sich aus den individuellen Budgetrestriktionen. Bezeichnet xe(p) die beim Preisvektor p = (pi, p2...., PO für Haushalt h optimale Konsummenge des Gutes g, ee die Anfangsausstattung des h mit Gut g, so gilt in einer Ökonomie ohne Produktion (unter geeigneten Annahmen über die Präferenzen der Haushalte) für jeden Haushalt h die Gleichung der Bilanzgerade:
WALRASsches Gesetz

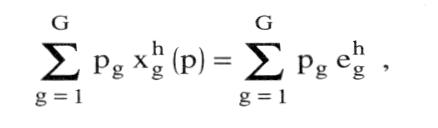Summation über alle h ergibt, wenn alle Gewinne vollständig ausgeschüttet werden (d.h. Eh dh = I für jedes u), das WALRASsche Gesetz:
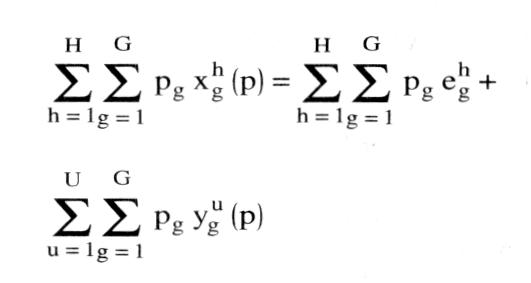WALRASsches Gesetz

Bezeichnet
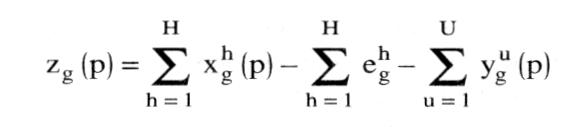WALRASsches Gesetz

die aggregierte Überschußnachfrage nach Gut g, so läßt sich das WALRASsche Gesetz komprimierter schreiben als:
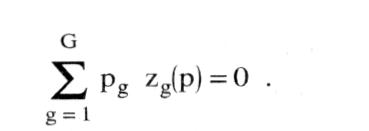WALRASsches Gesetz

Eine alternative Formulierung des WALRASschen Gesetzes lautet daher, dass der Wert der (über alle Märkte und Wirtschaftssubjekte) aggregierten Überschuß-nachfragen gleich Null ist. Zu beachten ist, dass das WALRASsche Gesetz bei beliebigen Preissystemen p (also nicht etwa nur im - Gleichgewicht) gilt. Eine wichtige Folgerung ist, dass Gleichgewicht auf G-1 Märkten (also etwa zg(p) = 0 für g = 1,..., G-1) Gleichgewicht auf dem G-ten Markt impliziert. Wird etwa angenommen, dass es nur vier Güter Arbeit, Sozialprodukt, Wertpapiere und Geld gibt, so muss der Geldmarkt im Gleichgewicht sein, falls es die drei übrigen Märkte sind. Das WALRASsche Gesetz steht im engen Zusammenhang mit bestimmten Formulierungen des - SAYschen Theorems.

Bei einer Totalanalyse muss in einem System von n Märkten auf dem n-ten Markt Gleichgewicht herrschen, wenn auf n — 1 Märkten ein Gleichgewicht existiert. Das Walras-Gesetz wird aus der —Budgetrestriktion rational planender Wirtschaftssubjekte abgeleitet. Aggregiert man diese Budgetrestriktionen über alle Wirtschaftssubjekte (einschl. Staat), so ergibt sich daraus zwingend, dass auch die Summe der wertmässigen Überschussnachfrage für alle Wirtschaftssubjekte auf allen Märkten identisch gleich Null ist (z. T. wird diese Aussage bereits als "Walras-Gesetz" bezeichnet, z.T. aber auch als "Walras-Identität"). Ist nun zusätzlich auf n — 1 Märkten die Überschussnachfrage gleich Null (Gleichgewicht), so muss auch auf dem n — ten Markt die Überschussnachfrage gleich Null sein. In einer geldlosen reinen Tauschwirtschaft entspricht das Walras-Gesetz dem Sayschen Gesetz. Aus dem Walras-Gesetz folgt die —Adding-up-Restriktion für die partiellen Ableitungen der Nachfragefunktionen in der —makroökonomischen Modellanalyse. Literatur: Fuhrmann, W., Makroökonomik, 3. Aufl., München, Wien 1991.

Vorhergehender Fachbegriff: Walrasianisches Gleichgewicht | Nächster Fachbegriff: WAMU

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Trump dekoriert Rasen vorm Weißen Haus mit Porträts abgeschobener Illegaler

Nachdem die selbsternannten Philanthropen der US-“DemonRatten” beim Thema Abschiebung illegaler und schwerkrimineller Migranten immer unsinnigere Argumenten aufbieten ihren Protest am Köcheln halten, hat die Trump-Administration gestern mit einer originellen Aktion dagegengehalten: Rund ums Weiße Haus in Washington D.C. wurden eine große Anzahl Schilder aufgestellt, die die Gesichter inhaftierter oder bereits abgeschobener krimineller illegaler Einwanderer zeigen. Damit hat […]

Wenigstens hier ist Deutschland Spitzenreiter: Rekordausgaben von 46,9 Milliarden für Bürgergeld

Eine Auswertung der Bundesagentur für Arbeit hat ergeben, dass 2024 die Rekordsumme von 46,9 Milliarden Euro an Bürgergeld ausgezahlt wurde. Während die Arbeitslosenzahlen nicht massiv steigen, ist dies bei den Transferzahlungen sehr wohl der Fall. Und der Hauptgrund ist natürlich auch hier die millionenfache Massenmigration in die Sozialsysteme. Im Schicksalsjahr 2015 lag die Summe der Sozialleistungen […]

Erleichterung: Trump wird kein Papst – aber immer mehr Muslime Polizisten

Ein satirischer Beitrag als Gedankensplitter von Peter Romberg Ein Aufatmen der Erleichterung geht derzeit durch die katholische Welt – auf die Nachricht hin, dass der US-Präsident Donald Trump inzwischen von seiner Forderung Abstand genommen hat, selbst das Amt des Papstes zu übernehmen. Stattdessen liegt nun von seiner Seite ein ultimativer Vorschlag auf dem Tisch, ohne […]