Bayes-Theorem

(Bayessches Theorem): Das in seiner einfachsten Form aus dem Multiplikationstheorem der Wahrscheinlichkeitstheorie abgeleitete Theorem, nach dem für zwei Ereignisse A und B gilt.

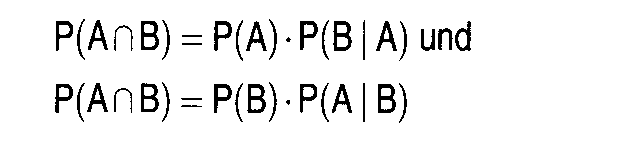Durch Gleichsetzung der beiden rechten Seiten ergibt sich das Bayes-Theorem: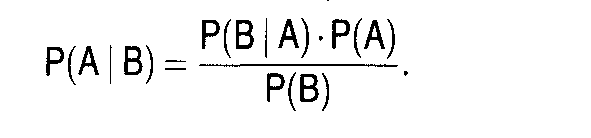

Es stellt die Regel für die Berechnung der Wahrscheinlichkeit dar, dass A eingetreten ist, wenn bekannt ist, dass B eingetreten ist. Für den Fall eines Ereignissystems mit N Ereignissen B1 bis BN ergibt sich die bedingte Wahrscheinlichkeit P(B.IA) durch Einsetzen der Ereigniswahrscheinlichkeit P(B,) als a-priori-Wahrscheinlichkeit in die Formel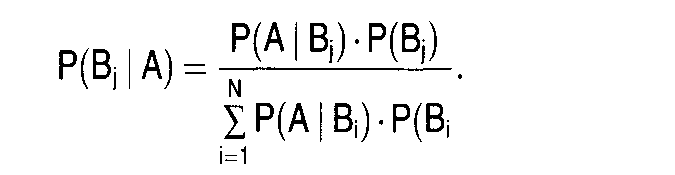

Bayes-Theorem

Sie gibt die a-posteriori-Wahrscheinlichkeit für B an, nachdem das Ereignis A eingetreten ist. Esbietet sich so die Möglichkeit, a-priori-Wahrscheinlichkeiten mit Hilfe der Beobachtung von Daten zu a-posteriori-Wahrscheinlichkeiten umzuformen. Anwendungsbereiche sind vor allem die statistische Entscheidungstheorie und die Stichprobenstatistik.

Informationswert

(Bayes-Regel) E bezeichne ein beliebiges Ereignis (Zufallsexperiment) in einem Ereignisraum S, der durch n sich gegenseitig ausschliessende Ereignisse Aj (i = 1, 2,..n) vollständig ausgefüllt wird. Unter diesen Voraussetzungen gilt das Bayessche Theorem 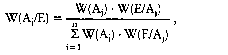Bayessches Theorem

das auf Thomas Bayes (1702-1761) zurückgeht. Wenn bekannt ist, dass das Ereignis E eingetreten ist, kann nachträglich die (bedingte) Wahrscheinlichkeit dafür, dass gleichzeitig das Ereignis Aj (j = 1,2,..., n) eingetreten ist, bestimmt werden. Man nennt die Wahrscheinlichkeit W(Aj/E) daher auch a- posteriori-Wahrscheinlichkeit des Ereignisses Aj. Die Wahrscheinlichkeit W(Aj) heisst im Gegensatz dazu die a-priori-Wahrscheinlichkeit. Wichtige Anwendungsbeispiele des Bayesschen Theorems sind Schätz- und Testverfahren mit Vorinformationen, die zu dem Gebiet der sog. Bayesschen Statistik gehören, sowie die präskriptive Entscheidungstheorie (|x-Prinzip). Literatur: Bleymüller; J./Gehlert, G./Gülicher, H., Statistik für Wirtschaftswissenschaftler, 8. Aufl., München 1992.

Vorhergehender Fachbegriff: Bayes-Regel | Nächster Fachbegriff: Bayes’sches Theorem

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Gewerke | Deutsche Zentralbibliothek für Wirtschaftswissenschaften | EUROTRA

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer