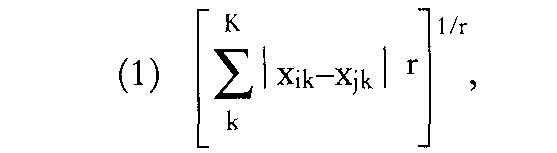Mehrdimensionale Skalierung (MDS)

Verfahren der Interdependenzanalyse in der Multivariatenanalyse zur Ermittlung der grundlegenden Merkmalsdimensionen, auf denen Stimuli differenziert oder beurteilt werden. Es wird im Marketing zur Identifikation der Positionen von Produkten (Stimuli) auf diesen Merkmalsdimensionen eingesetzt, wobei die Relationen der Produkte über eine Punktekonfiguration in zwei oder drei Dimensionen räumlich abgebildet werden können (Positionierung). Erfaßt man Wahrnehmungen, bezeichnet man die grafische Repräsentation als Wahrnehmungsraum. Die Abb. veranschaulicht als Beispiel den Wahrnehmungsraum von Hausfrauen für Backprodukte. Die relevanten Merkmalsdimensionen sind Preisgünstigkeit und Qualität (Frische und Zutaten). Alternativ lassen sich auch Präferenzen ab- fragen, wobei die Dimensionen den Präferenzraum des Befragten aufspannen (Positionierungsmodell). Im sog. Joint Space werden Ähnlichkeiten zwischen Stimuli und Präferenzdaten integriert. Eine weitere Möglichkeit ist die Einbeziehung von Idealpunkten, d. h. hypothetischen Stimuli mit höchster Präferenz (Kaufmodell). Ausgangsbasis der allgemeinen MDS ist eine Dreiecksmatrix mit Koeffizienten für die wahrgenommene Ähnlichkeit bzw. Unähnlichkeiten zwischen Stimulipaaren. Man unterscheidet je nach Skalenniveau der Ausgangsdaten metrische und nichtmetrische MDS. Methoden der Datenerhebung stellen der Paarvergleich, Ähnlichkeitsratings und die Ankerpunktmethode dar. Hierbei sind jeweils Produktpaare nach Ähnlichkeit oder Präferenz zu ordnen oder zu beurteilen. Werden die Objekte nach Präferenz (Unfol- ding) geordnet, unterstellt man implizit, dass das erst- und zweitpräferierte Objekt am ähnlichsten sind, dagegen das erst- und letzt- präferierte Objekt die größte Unähnlichkeit aufweisen. Die Positionierung eines Stimulus erfolgt über die Transformation der Ähnlich- keitsdaten in ein Distanzmodell. Hier sollen geringe Distanzen von Stimuli eine große Ähnlichkeit signalisierenundumgekehrt. Ein MDS-Algorithmus umfaßt mit einem Distanz-Modell und einer MDS-Schätz- funktion mindestens zwei Modell-Komponenten. Unter Vorgabe der Dimensionsanzahl (meist zwei) wird eine Ausgangskonfiguration der Stimuli solange verbessert, bis eine möglichst gute Anpassung an die beobachteten Daten erreicht ist. Man unterscheidet metrische und nichtmetrische Verfahren. In den meisten MDS-Verfahren hat die Beziehung der Positionen zweier Objekte und ihre Distanz die Form einer Minkowski- Metrik:
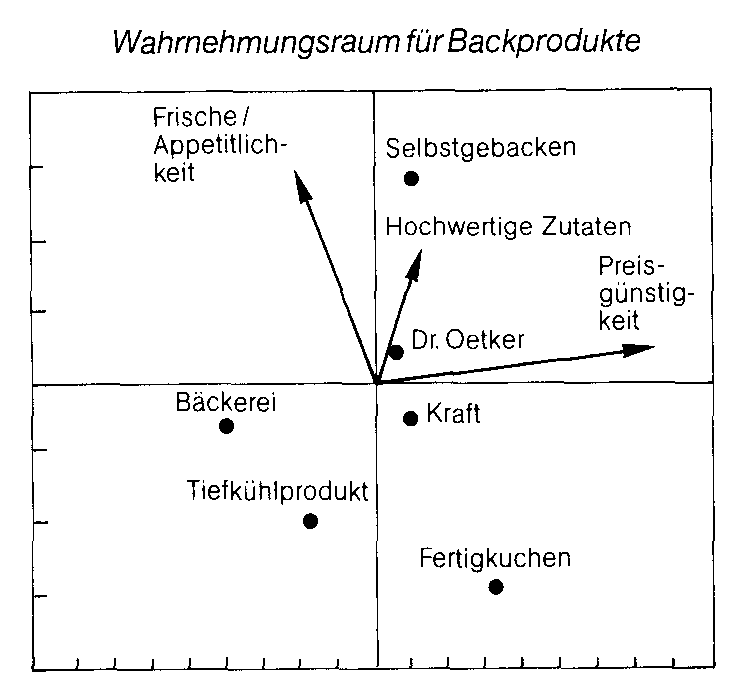Mehrdimensionale Skalierung (MDS)

mit

Ein Metrik-Parameter von r = 2 bestimmt die im Rahmen der MDS häufig eingesetzte Euklidische Metrik. Die City-Block-Metrik ergibt sich bei r = 1, während man bei r = °° von Supremiums-Metrik spricht. Unter Vorgabe der Metrik werden auf Grundlage der Ahn- lichkeitsdaten die Distanzen geschätzt. Der MDS-Algorithmus bestimmt die unbekannte Beziehung f zwischen beobachteter Ähnlichkeit und theoretischer Distanz. (2)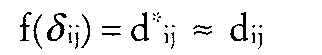
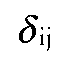Mehrdimensionale Skalierung (MDS)

mit beobachtete Ähnlichkeit zwischen Ob
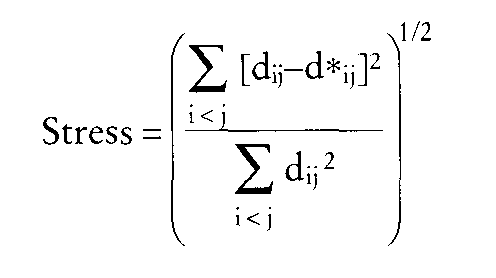Mehrdimensionale Skalierung (MDS)

jekt i und j, di, theoretische Distanz zwischen i und j, d‘ ij über f(öij) transformierte Ähnlichkeitsdaten. In der metrischen MDS hat die Beziehung f((5;j) die Form eines Polynoms n-ten Grades. In der nichtmetrischen MDS handelt es sich um eine schwach monotone Funktion. Für eine vorgegebene Dimensionsanzahl und eine Startkonfiguration bestimmt der MDS- Algorithmus die Stimuluskonfiguration (Konfiguration), die über die geschätzte Funktion eine möglichst gute Anpassung an die beobachteten Daten ermöglicht. Die Güte der Anpassung läßt sich, sofern keine degenerierte Lösung vorliegt, anhand des Stress-Wertes oder des Shepard-Dia- gramms beurteilen. Der Stress-Wert wird bei der Schätzung der Funktion als das zu minimierende Zielkriterium herangezogen. In den meisten MDS- Algorithmen werden Varianten des Kruskal- Stress eingesetzt:
Mehrdimensionale Skalierung (MDS)

Als schlechte Modellanpassung gilt, wenn der Stress-Index größer als 0,2 ist. Die Höhe des Stress-Wertes sinkt in aller Regel mit abnehmender Zahl der Objekte sowie mit steigender Zahl der Dimensionen. Neben MDS-Verfahren, die eine einzige (individuelle oder aggregierte) Datenmatrix analysieren, existieren MDS-Algorithmen wie INDSCAL (Individual Differences Scaling), die mehrere Datenmatrizen simultan als N- oder Mehr-Wege-Analyse verarbeiten. Mehr-Wege-Daten liegen z.B. vor, wenn die Information einer Distanzmatrix z.B. über mehrere Personen oder zu verschiedenen Zeitpunkten repliziert wird und individuelle bzw. zeitpunktspezifische Unterschiede erfaßt werden. Interpretationsmöglichkeiten eines MDS- Raums bietet die Facettentheorie oder die explizite Integration von extern erhobenen Eigenschaftsurteilen über Analyseprogramme wie PROFIT (Property Fitting). Die Produktpositionen der Lösungskonfiguration werden bei PROFIT auf Eigenschaftsbewertungen regressiert, um diese als Eigenschaftsvektoren in den Wahrnehmungsraum zu legen. Die auf den Vektor projezierten Stimulusdistanzen zeigen die eigenschaftsspezifischen Wahrnehmungs- unterschiede. Die Rotation des Wahrnehmungsraumes ermöglicht zudem, die Eigenschaftsvektoren auf die Raumdimensionen zu legen. Die exploratorischen MDS-Analysen sind heute durch Programme zur Konfirmatorischen MDS erweitert worden. Sie ermöglichen es, Hypothesen über die Konfiguration der Stimuli im Wahrnehmungsraum mit einzubeziehen und zu testen (Borg und Lingoes). Der Test erfolgt über Restriktionen, die auf die MDS-Konfigurationen gelegt werden. Teststatistiken und Fitindices liefern Anhaltspunkte über den Grad der Abweichungen einer MDS-Lösung von einer hypothetischenZielkonfiguration. Ähnliches leistet der PROSCAL-Ansatz zur Schätzung von probabilistischen Konfigurationen. Ihr Vorteil ist die Explikation eines Fehlermodells für die beobachteten Ähnlichkeitsdaten. Sind die Annahmen über das Fehlermodell gerechtfertigt, können die Parameter mit der Maximum-Likelihood- Methode geschätzt werden. Während die deterministische MDS nur Schätzer für die Stimulikoordinaten liefert, schätzt die probabilistische MDS dann sowohl die Position als auch die Unsicherheit der Position eines Stimulis im Raum. Der Ansatz liefert gleichzeitig einen Signifikanz-Test für den Grad der Modellverbesserung bei Berücksichtigung einer zusätzlichen Dimension.

Literatur: Borg, I.; Lingoes,]. C., A Model and Al- gorithm for Multidimensional Scaling with Exter- nal Constraints on the Distances, Psychometrika, 45.Jg. (1979) S.25-38. Dichtl E.; Schobert R.,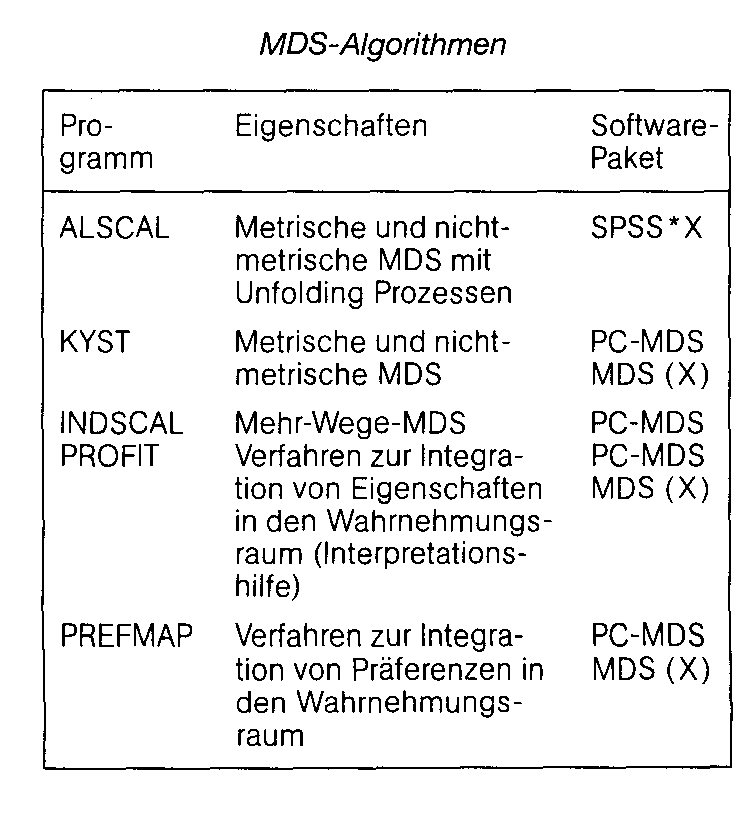
Mehrdimensionale Skalierung (MDS)

Die Tabelle gibt eine kurze Charakterisierung wichtiger MDS-Algorithmen. Mehrdimensionale Skalierung. Methodische Grundlagen und betriebswirtschaftliche Anwendungen, München 1979. Green, P.E.; Carmone, F.J.Jr.; Smith, , Multidimensional Scaling: Concepts and Applications, Boston 1989. Kruskal, J.B., Multidimensional Scaling by optimizing Goodness of Fit to a nonmetric Hypothesis, in: Psychometrica, 29.Jg. (1964) S. 1-27. Schiffman, S. S.; Reynolds, M. L.; Young, , Introauction to Multidimensional Scaling. Theory, Methods and Applications, New York 1981, S. 59 f.

Vorhergehender Fachbegriff: mehrdimensionale Skalierung | Nächster Fachbegriff: Mehrdimensionaler Produktraum

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Hauptrefinanzierungsgeschäft | Beschaffungsinstrumente | Arbeitseinkommen

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer