Binomialverteilung

Tritt in einer Serie paarweise unabhängiger Versliche je Versuch ein Merkmal (z. Binomialverteilung »Beleg fehlerhaft«) mit der (konstanten) » Wahrscheinlichkeit p auf und mit q = 1p nicht auf (z. Binomialverteilung »Beleg fehlerfrei«), dann ist die Wahrscheinlichkeit, daß dieses Merkmal in n Verslichen genau xmal auftritt, gegeben durch eine Binomialverteilung von der Ordnung n mit dem Parameter p, deren Dichtefunktion fB(xln; p) {(„y(lPrfürx = l V 0, l,. . ., n über folgende Rekursionsformel tabelliert werden kann: fB(0ln; p) qn; (fB(x+lln; p) £fB(xln; p); x0, l,. . ., n. Der Erwartungswert beträgt E(X) = np und die Varianz V(X) = npq. Obwohl die Binomialverteilung das »Zurücklegen« der gezogenen Einzelprobe unterstellt und daher der Prüfungsrealität nicht voll gerecht wird, hat sie gegenüber der » Hypergeometrischen Verteilung den Vorteil der leichteren Tabellierbarkeit. Für n «» geht sie in diese über und kann daher zu deren Approximation herangezogen werden.

In der Wirtschaftssoziologie: Wahrscheinlichkeitsfunktion, die die Wahrscheinlichkeit angibt, dass bei zwei möglichen Ereignisarten, A oder B, das Ereignis A bei n Versuchen (z.Binomialverteilung ziehen einer Kugel aus einer Urne mit schwarzen oder weissen Kugeln) x-mal eintritt. Die Erfolgswahrscheinlichkeit von A beim Einzelversuch sei p. q = 1 - p sei die Wahrscheinlichkeit, dass sich B ereignet. Da die Einzelergebnisse unabhängig sind, ist die Wahrscheinlichkeit einer Form der Realisierung von x: p“ q“-x = p p p p ...p q q q ... q ;t-mal n - *-mal Da es für x mögliche Realisierungsformen gibt, ergibt sich die Wahrscheinlichkeit von x aus:

eine der ältesten theoretischen Verteilungen der Statistik; sie geht auf Jakob Bernoulli (1654-1705) zurück und wird deshalb auch oft als Bernoulli-Verteilung bezeichnet. Betrachtet man ein Bernoulli-Experiment mit n Einzelversuchen, wobei die Wahrscheinlichkeit für Ereignis A W(A) = 0 beträgt, dann ist die Wahrscheinlichkeit, dass bei den n Einzelversuchen genau x-mal Ereignis A auf- tritt, durch die Wahrscheinlichkeitsfunktion der Binomialverteilung gegeben: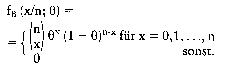

Die Form der Binomialverteilung wird durch die numerischen Werte ihrer Parameter n und 0 bestimmt. Für 0 = 0,5 ist die Verteilung symmetrisch; für n °° erhält man als Grenzverteilung die Normalverteilung (Approximationen). Die Binomialverteilung dient in der Stichprobentheorie zur Berechnung von Wahrscheinlichkeiten für das Urnenmodell mit Zurücklegen für ein binäres (dichotomes) Merkmal, d.h. ein nominalskaliertes Merkmal (Skala) mit nur zwei Ausprägungen. Ein wichtiges Anwendungsbeispiel ist die Gut-Schlecht-Prüfung im Rahmen der statistischen Qualitätskontrolle. J. BUG. G. Literatur: Bleymüller, J.lGehlert, G./Gülicher, H., Statistik für Wirtschaftswissenschaftler, 8. Aufl., München 1992.

(Bernoulli-Verteilung): Eine Wahrscheinlichkeitsverteilung für diskrete Variablen mit nur zwei möglichen Ausprägungen A und A, die mit der Wahrscheinlichkeit p und 1— p auftreten. Die Binomialverteilung gibt für jeden beliebigen Variablenwert x aus N Fällen die Wahrscheinlichkeit P(x) an, dass von N Ereignissen x-mal A und N — x-mal A eintritt: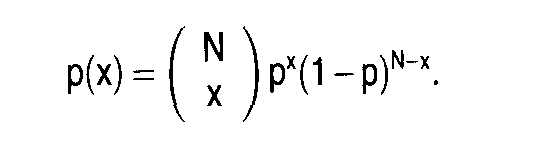

Durch die Binomialverteilung wird das klassische Urnenmodell der Stichprobentheorie mit weißen und roten Kugeln und einer Auswahl mit Zurücklegen erfaßt. Sie ist somit eine der Fundamentalverteilungen der Stichprobentheorie, für die zahlreiche Anwendungen bei dichotomen Grundgesamtheiten bestehen. Die Binomialverteilung ist im Gegensatz zur Normalverteilung asymmetrisch. Ihre Schiefe wird jedoch mit wachsendem N geringer, bis sie bei sehr großen N in die Normalverteilung übergeht.

Vorhergehender Fachbegriff: Binnenzollstelle | Nächster Fachbegriff: Biographischer Fragebogen

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : heterogene Kostenverursachung | Güterverkehr | Organisationsberatung

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer