Haushaltsoptimum

Güterkombination, die ein Wirtschaftssubjekt bei gegebener Konsumsumme sowie gegebenen Güterpreisen nachfragt, wenn es versucht, das Nutzenmaximum zu erreichen. Das Wirtschaftssubjekt setzt somit seine knappen Mittel effizient ein und versorgt sich unter den gegebenen Bedingungen am besten.

haushaltsoptimum

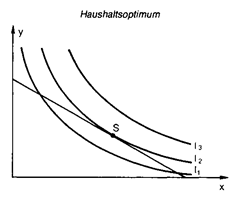Diese optimale Güterkombination ergibt sich, indem die Steigung der maximal erreichbaren Indifferenzkurve (I₂) mit der der Bilanzgeraden (Budgetlinie) übereinstimmt (Punkt S in Abb.), d.h. die Grenzrate der Substitution (dy:dx) gleich dem negativen reziproken Verhältnis der Güterpreise ist: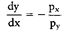

haushaltsoptimum

Die Grenzrate der Substitution ist nun jedoch gleich dem negativen reziproken Verhältnis des Grenznutzens beider Güter, so dass auch gilt:

Durch Umformung erhält man j d.h. eine Gleichheit des gewogenen Grenznutzens (Grenznutzen des Geldes) der beiden Güter (Zweites Gossensches Gesetz).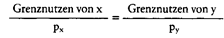

Das Haushaltsoptimum ist die Grundlage für die Ableitung der individuellen Nachfragekurve. Ausserdem spielt es eine sehr wesentliche Rolle in der Wahlhandlungstheorie.

Literatur: Fehl, Oberender, P., Grundlagen der Mikroökonomie, 5. Aufl., München.

(= Haushaltsgleichgewicht) Güterkombination, die ein Haushalt bei gegebener Konsumsumme und gegebenen Güterpreisen verbraucht, wenn das höchstmögliche Versorgungsniveau oder Nutzenmaximum (-f Indifferenzkurven) angestrebt wird. Das Haushaltsoptimum ist im Tangentialpunkt P (mit den Mengen y und i) von Bilanzgerade und höchsterreichbarer Indifferenzkurve gegeben, wobei die Bilanzgerade zur Substitutionstangente wird. Dann gilt d.h., die Grenzrate der Substitution (Indifferenzkurven) ist gleich dem negativen reziproken Verhältnis der Güterpreise. Da die Grenzrate der Substitution gleich dem (negativen) reziproken Verhältnis der Grenznutzen (Nutzen) beider Güter ist, kann die Bedingung für das Haushaltsoptimum auch geschrieben werden: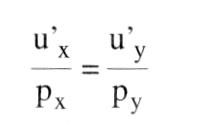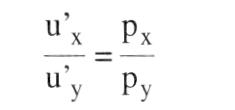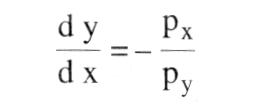

Das Verhältnis der Grenznutzen (u\') der Güter x und y ist gleich dem Preisverhältnis, woraus nach Umformung in das zweite GOSSENsche Gesetz als Bedingung für das Haushaltsoptimum entwickelt werden kann.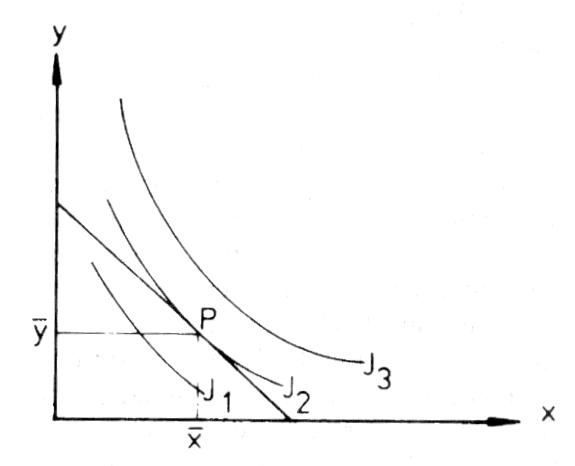

Die Herleitung des Haushaltsoptimums ist Gegenstand der auf dem ordinalen Nutzenkonzept (Nutzenmessung) aufbauenden - Wahlhandlungstheorie und Grundlage für die Bestimmung der individuellen Nachfragekurve. Im Falle von Rationierung sind die Bedingungen des Haushaltsoptimums u.U. nicht erfüllt (Doppelkeildiagramme). Literatur: Linde, R. (1992). Schumann, J. (1992). Varian, H.R. (1994)

Vorhergehender Fachbegriff: Haushaltskreislauf | Nächster Fachbegriff: Haushaltsordnung

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Sonderanlässe der Finanzierung | collective-bargaining-Theorie | Datenbanksysteme

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer