Durchdringungsmodelle

(Marktdurchdringungsmodelle): Sammelbezeichnung für eine Reihe von Modellen zur Prognose von Marktanteilen und Erstkäufen, in denen der Anteil der Käufer, die ein Produkt wenigstens einmal gekauft haben, als Durchdringung oder Marktdurchdringung bezeichnet wird, der im Zeitverlauf einen Grenzwert annimmt.
Durchdringungsmodelle dienen z.B. zur Abschätzung künftiger Marktanteile in Testmärkten.
Grundsätzlich ist zwischen einfachen geometrischen Durchdringungsmodellen (L. A. Fourt & J. W. Woodlock) und exponentiellen Durchdringungsmodellen (J. H. Parfitt & B. J. K. Collins) zu unterscheiden.
Das von Fourt & Woodlock 1960 formulierte Modell nimmt an, dass der Zuwachs der Erstkäufer mit der Zeit abnimmt und dass ihre kumulierte Gesamtzahl einen deutlich unterhalb der Zahl der Mitglieder des Haushaltspanels im Testmarkt liegenden Grenzwert annimmt.
Der Zuwachs (At) der Marktdurchdringung in einer Periode ist danach proportional zum insgesamt erreichbaren Grenzwert der Erstkäufer (a): At=13a(1 -13t-1).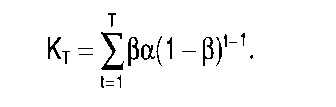

Durchdringungsmodelle

Darin bezeichnet a einen im Zeitverlauf konstanten Käuferanteil, d.h. die Durchdringungsgrenze, und ss eine von Null verschiedene, im Zeitverlauf konstante und für alle Konsumenten gleich hohe Einkaufswahrscheinlichkeit. Es ergibt sich also für die kumulierte Zahl der Erstkäufer im Beobachtungszeitraum T:

Bei der Berücksichtigung von Wiederkäufen (Wiederholungskäufen) ist zwischen Wiederkauf-raten unterschiedlicher Ordnung zu unterscheiden. Der Anteil der Erstkäufer mit einmaliger Kaufwiederholung stellt die Wiederkaufrate erster Ordnung dar, der Anteil der Erstkäufer mit zweimaliger Kaufwiederholung die Wiederkaufrate zweiter Ordnung usw. Entsprechend gilt für die Wiederkauf rate Fix, des x-ten Kaufs im gesamten Beobachtungszeitraum:

Durchdringungsmodelle

Die Gesamtzahl der Käufer am Ende der Beobachtungsperiode ergibt sich entsprechend durch Multiplikation der prognostizierten Durchdringung und der Wiederkaufraten. “Aufgrund der kaufzahlabhängigen Bestimmung der Wiederholungskäufe sind relativ lange Beobachtungszeiträume erforderlich, so dass der Einsatz des Modells auf kurzlebige Verbrauchsgüter beschränkt ist. Problematisch ist auch die Annahme zeitlich konstanter Modellparameter. So hat sich in empirischen Anwendungen ergeben, dass das Modell dazu neigt, den Verlauf der Erstkäufe zu Beginn des Beobachtungszeitraums zu unterschätzen. Fourt und Woodlock (1960) sprechen von einem heavy-buyer-Effekt, den sie durch Addition einer heuristisch geschätzten Konstanten zu berücksichtigen trachten. Auch muss zusätzlich noch eine Schätzung der Kaufmengen pro Kauf erfolgen, damit das Modell eine Absatzprognose leisten kann.” (W. Beeskow/E. Dichtl/G. Finck/S. Müller)
Das 1968 formulierte gängige exponentielle Durchdringungsmodell von Parfitt & Collins gibt zunächst ganz ähnlich die kumulierte Zahl der Erstkäufer in der Beobachtungsperiode wie folgt an: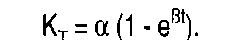

Durchdringungsmodelle

Anstelle der Annahme der Kaufzahlabhängigkeit der Wiederkauf rate geht dieses Modell jedoch von der Abhängigkeit von der Zeit nach dem Erstkauf aus. Die Durchführung des Parfittschen Modells zur Prognose des Marktanteils erfordert ebenfalls den Einsatz eines Verbraucherpanels. Dabei wird der langfristige Marktanteil (MA) als Produkt der Grenzrate der Durchdringung (Erstkäuferzahl) a, dem Grenzwert der Wiederkauf rate und der konstanten relativen Konsumintensität (Kaufintensität) i bei Stabilisierung der Marktdurchdringung berechnet: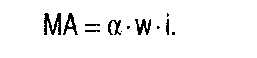

Durchdringungsmodelle

Der Grenzwert der Wiederkaufrate wird nach dem Parfittmodell durch graphische Extrapolation von periodenbezogenen Wiederkaufraten bestimmt (operationalisiert als Anteil der Wiederkaufmenge des Produkts an der Gesamtnachfrage in der entsprechenden Produktklasse).
“Als Hauptvorteil dieses Modells kann die getrennte funktionale Darstellung einzelner Determinanten des Marktanteils, die dadurch auch einzeln validierbar sind, genannt werden. Obwohl die Wiederkaufraten jetzt zeitabhängig und in Bezug auf die Gesamtnachfrage in der Produktklasse bestimmt werden, verbleiben auch in diesem Modell einige Mängel. Beispielsweise bleibt der Handel, für den man einen ähnlichen Durchdringungsprozess annehmen darf (kumulative Distribution), völlig unberücksichtigt. Eine weitere Schwachstelle liegt auch bei diesem Modell in der Notwendigkeit begründet, einen relativ langen Beobachtungszeitraum (etwa 1 Jahr) abwarten zu müssen, um zuverlässige Schätzungen via Extrapolation des Datenmaterials zu erhalten. Damit dürfte allerdings die Annahme stabiler Marketingaktivitäten sowohl seitens der Konkurrenten als auch seitens der Unternehmung selbst zur reinen Fiktion werden.” (W. Beeskow/E. Dichtl/G. Finck/S. Müller)

Vorhergehender Fachbegriff: Durchdringung | Nächster Fachbegriff: Durchführbarkeitsstudie

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : MXN | Lofo-Methode | Waldbesitzstruktur

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer