Bernoulli-Prinzip

Das Bernoulli-Prinzip stellt eine Erweiterung des Bayes-Prinzips dar. Bernoulli führte ein zusätzliches Kriterium neben den Eintrittswahrscheinlichkeiten der Umweltsituationen ein, nämlich die subjektive Nutzenbewertung über eine Nutzenfunktion der möglichen Alternativen durch den Entscheidungsträger. Die einzelnen Aktionen werden nunmehr aufgrund des zugehörigen Nutzen-erwartungswertes beurteilt. Da dieser jeweils eine reelle Zahl ist, werden alle Aktionen miteinander vergleichbar. Die für das Bernoulli-Prinzip typische Nutzenfunktion wird auch als Bernoulli-Nutzen, als Risiko-Nutzen oder als von Neumann-Morgenstern-Nutzen bezeichnet.

Entscheidungsregel, Erwartungswert

Entscheidungsregel der präskriptiven Entscheidungstheorie für Risikosituationen. Danach werden sämtliche mit den zur Auswahl stehenden Handlungsalternativen aj verbundenen Ergebnisse ejj mittels einer Ri- siko-Nutzen-Funktion U(e) in Nutzenwerte ujj umgerechnet. Als optimal gilt dann die Alternative, für die sich der maximale mathematische Erwartungswert der zugehörigen Nutzenwerte ergibt. Die Entscheidungsregel lautet also 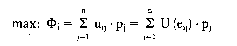Bernoulli-Prinzip

wobei die pj die den einzelnen e zugeordneten Eintrittswahrscheinlichkeiten bezeichnen. Wird die Risiko-Nutzen-Funktion U(e) durch eine lineare Transformation Ü(e) = a 4- b • U(e) mit b 0 ersetzt, so ergibt sich auf der Basis von Ü(e) zwangsläufig die gleiche Rangfolge der Alternativen a; wie bei Verwendung von U(e). Mithin kann die verwendete Risiko-Nutzen-Funktion durch jede beliebige positiv-lineare Transformation ersetzt werden. Die Risiko-Nutzen-Funktion selbst wird durch das Bernoulli-Prinzip nicht vorgegeben, sondern ist je nach den Höhen- und Risikopräferenzen des Entscheidungssubjekts zu gestalten, so dass das Bernoulli-Prinzip je nach dem Verlauf der zugrundegelegten Risiko- Nutzen-Funktion durchaus unterschiedliche Formen der Risikoeinstellung zum Ausdruck bringen kann. Verläuft die Risiko-Nutzen-Funktion linear, so stimmen Sicherheitsäquivalent und mathematischer Erwartungswert überein. Diese Verlaufsform impliziert also Risikoneutralität; das Bernoulli- Prinzip stimmt für diesen Spezialfall mit dem |x-Prinzip überein. Ein degressiv (progressiv) steigender Verlauf der Risiko-Nutzen- Funktion führt demgegenüber dazu, dass der mathematische Erwartungswert grösser (kleiner) ist als das Sicherheitsäquivalent, impliziert also Risikoaversion (Risikobereitschaft). Im konkreten Anwendungsfall kann der Verlauf der benötigten Risiko-Nutzen-Funk- tion der sog. Bernoulli-Befragung in folgender Weise aus einfachen hypothetischen Wahlakten des Entscheidungssubjektes abgeleitet werden: Das Entscheidungssubjekt wird vor die Wahl gestellt zwischen den Alternativen: a_a: Erzielung des sicheren Ergebniswertes e, a₂: Möglichkeit, mit der Erfolgswahrschein- lichkeit p das bessere Ergebnis e" und mit der Gegenwahrscheinlichkeit (1 — p) das schlechtere Ergebnis e\' zu erzielen (e" e e). Für die Präferenzwerte dieser beiden Alternativen gilt allgemein Cp ₂ = U(e) und (p₂ = P * U (e") + (1 - p) • U(e\'); allerdings sind die U-Werte zunächst noch gar nicht bekannt. Angesichts der Invarianz des Aussagegehaltes der Risiko-Nutzen-Funktion U(e) gegenüber beliebigen positiv-linearen Transformationen ist es ohne Einschränkung der Allgemeinheit möglich, den Ergebniswerten e" und e\' die Nutzenwerte U(e") = 1 und U(e\') = 0 zuzuordnen; für (J)₂ gilt dann einfach (p₂ = p. Um auf der Basis der so vorgenommenen Normierung der Risiko-Nutzen-Funktion auch U (e) zu bestimmen, wird die Erfolgswahrscheinlichkeit für a₂ so lange variiert, bis der kritische Wert p(e) gefunden ist, bei dem 2li und a₂ gerade als gleichwertig angesehen werden. Äquivalenz von ai und a₂ bedeutet aber, dass (pi = (p₂ und damit U(e) = p(e) gelten muss. In entsprechender Weise kann für beliebige andere e-Werte (e" e e\') jeweils die zugehörige Erfolgswahrscheinlichkeit p(e) ermittelt und damit zugleich die Risiko-Nut- zen-Funktion in beliebig vielen Punkten bestimmt werden. Das Bernoulli-Prinzip kann als zwingende Implikation bestimmter, relativ einfacher Axiome aufgefasst werden. Akzeptiert man die jeweiligen Axiome als vernünftige Anforderungen an die Qualität einer Entscheidungsregel für Risikosituationen, so ergibt sich daraus zwingend, dass die Entscheidungsregel mit dem Bernoulli-Prinzip kompatibel ist. Es sind verschiedene Axiomen-Systeme entwickelt worden, die das Bernoulli-Prinzip implizieren. Eines der einfachsten besteht aus dem Ordinalaxiom, dem Stetigkeitsaxiom und dem Substitutionsaxiom. Während Ordinal- und Stetigkeitsaxiom als "vernünftige" Anforderungen an eine Entscheidungsregel weithin akzeptiert werden, ist die Plausibilität des Substitutionsaxioms umstritten. Literatur: Bitz, M., Entscheidungstheorie, München 1981, insb. S. 153 ff. Laux, H., Entscheidungstheorie. Grundlagen, Berlin u.a. 1982, insb. S. 169ff. Schneeweiss, H., Entscheidungskriterien bei Risiko, Berlin u.a. 1967.

Vorhergehender Fachbegriff: Bernoulli-Maxime | Nächster Fachbegriff: Bernoulli-Regel

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Stop-buy-order | Tiger | Hauptrefinanzierungsinstrument

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer