LISREL

Das Softwareprogramm LISREL (Linear Structural Relationships) ist ein Programm zur Analyse von Kausalmodellen (Kausalanalyse). Es war eines der ersten Computerprogramme für diese statistische Methode. Von den vorliegenden Programmen hat es bisher die weiteste Verbreitung gefunden. Alternative Systeme von Bedeutung sind EQS, SEPATH und AMOS (vgl. Homburg/Hildebrandt, 1998, S. 18).

In der Wirtschaftssoziologie: kurz für: Linear Structural Relationships, von K.G. Jöreskog und D. Sörbom entwickelter Ansatz zum Testen von theoretisch konstruierten Hypothesensystemen. Ausgehend von der Analyse von Korrelations- und Kovarianzbeziehungen werden Beziehungen zwischen latenten Variablen überprüft. Der Ansatz besteht aus einem Strukturmodell, in dem die Beziehungen zwischen den latenten Variablen formuliert werden, und je einem Messmodell für die exogenen und endogenen Indikatorvariablen. Die Abbildung der latenten Variablen im Strukturmodell folgt dem pfad- bzw. regressionsanalytischen Modell, während die Messmodelle dem faktoranalytischen Ansatz folgen; entsprechend wird ein metrisches Datenniveau vorausgesetzt. Muthen hat unter dem Namen LISCOMP ein Modell vorgestellt, das auch endogene Variablen ordinalen Niveaus zulässt. Für beide Modelle sind gleichnamige EDV- Programme verfügbar. C

(Analyse von Linear Structural Relationships) bezeichnet ein Computerprogramm und einen Modellansatz zur Zerlegung von Kovarianzstrukturen in der Multivaria- tenanalyse, das primär zur Kausalanalyse eingesetzt wird. Das Programm liegt 1990 in der siebten Version vor und beruht im Kern auf einer Ineinanderschachtelung von Faktoranalyse-Modellen, deren Parameter mit Maximum Likelihood oder Kleinste-Quadrate Methoden geschätzt werden können. LISREL stellt einen allgemeinen Ansatz dar, der eine Kovarianzmatrix von Daten als eine Funktion von Parametern eines theoretischen linearen Modells auffaßt und verschiedenartige Beziehungen zwischen Beobachtungsvariablen, Faktoren und Fehlerkomponenten gleichzeitig abbilden kann. Die Faktoren repräsentieren nicht direkt beobachtbare Konstrukte oder latente Variablen. Ein LISREL-Modell besteht aus drei Teilen, einem exogenen Meßmodell, einem endogenen Meßmodell und einem Strukturmodell (vgl. Abb.). Für die mathematische Spezifikation wird angenommen, dass alle Variablen als Abweichungen vom Mittelwert gemessen sind. Dadurch entfallen die Absolutglieder in den Gleichungen. Nach den Konventionen von LISREL VII für den Ein-Sample-Fall hat das Modell folgende Struktur: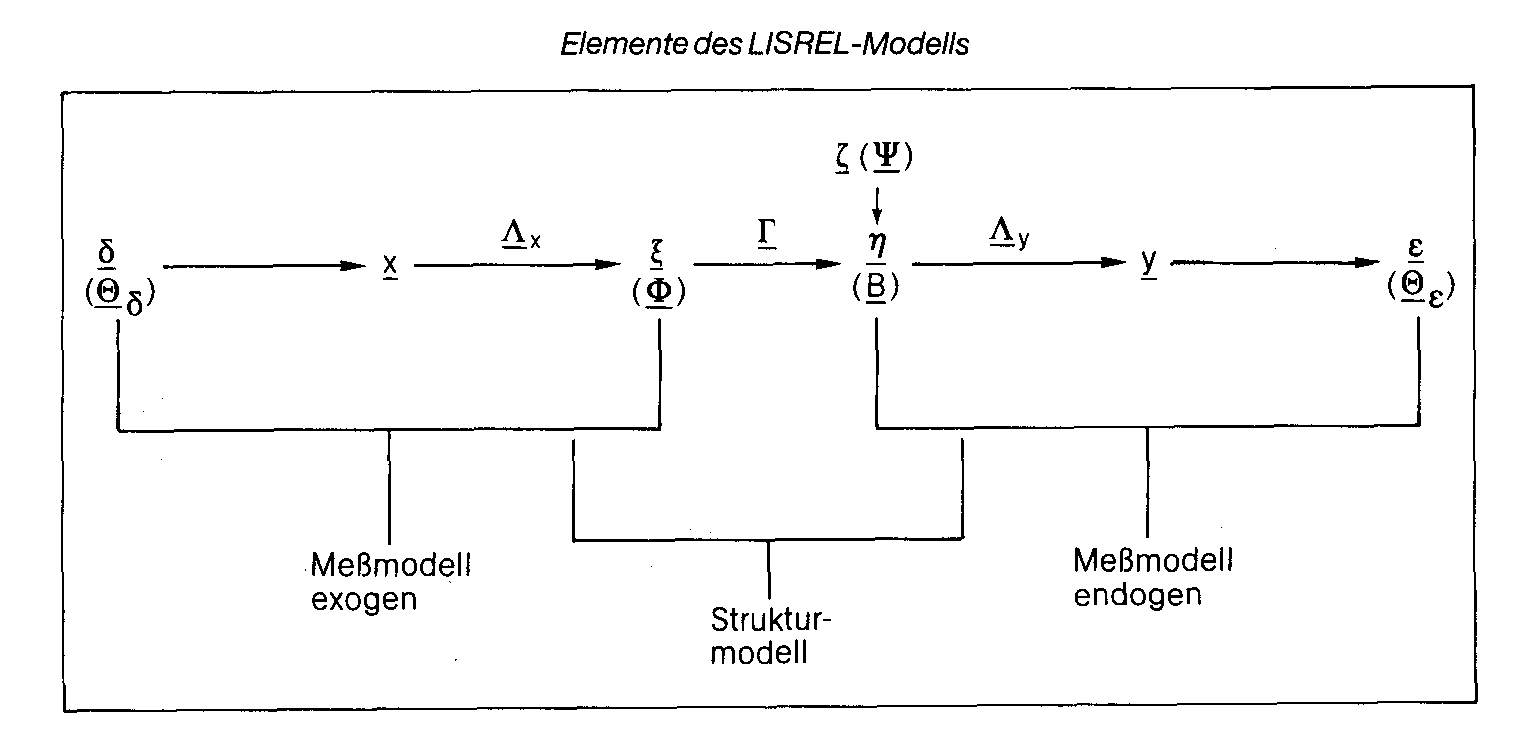
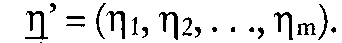LISREL

Die Variablen werden unterschieden nach Messungenx’= (xi,x2,.. .,xp) vonunabhängigen (exogenen) Konstrukten . . !;„) und Messungen y = (yi, y2, .. yq) von abhängigen (endogenen) Konstrukten
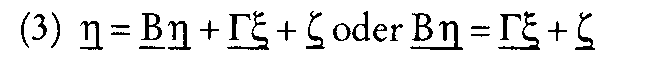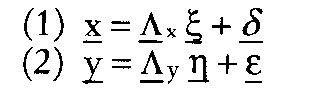LISREL

Durch zwei Faktormodelle
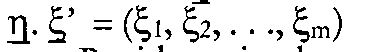LISREL

werden die Beziehungen zwischen den Beobachtungsvariablen (x, y) und den Konstrukten (£, T|) abgebildet, £ und 8 sind die Vektoren der Meßfehler von y und x. Die Matrizen Ay (qxm) und Ax(pxn) erfassen die Faktorladungen (Regressionsgewichte) von y auf r| sowie x auf Die kausalen Beziehungen werden durch ein System von linearen Strukturgleichungen auf der Konstruktebene modelliert: mit [‘B = (I-B)], hier ist B die (mxm) Koeffizientenmatrix für die direkten kausalen Beziehungen zwischen endogenen Konstrukten T[; und F, der (mxn) Koeffizientenmatrix für die direkten kausalen Beziehungen zwischen den exogenen Konstrukten£, und endogenen Konstrukten
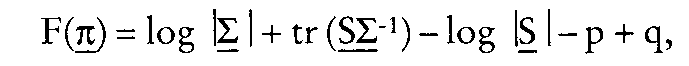LISREL

ist der Zufallsvektor von Kesiduen in den Kausalbeziehungen. Zur Lösbarkeit der Gleichungssysteme werden folgende Basis-Annahmen getroffen: e und S sind untereinander unkorreliert und unkorreliert mit rj, £ und £ ist unkorreliert mit den exogenen Konstrukten und die Matrix I-B ist nicht singulär. Das Programm schätzt Parameter unter Berücksichtigung von Restriktionen und Parametervorgaben in acht Parametermatrizen, die eine vollständige Modellstruktur abbilden. Dies sind neben den AbhängigkeitsbeZiehungen in Ax, Ay, B, £, die spezifizierten Kovariationsbeziehungen in:
LISREL

Sofern die Information in den Daten ausreicht, um alle Koeffizienten eindeutig zu bestimmen (Identifikation), können Kleinste-Quadrate Schätzmethoden (ULS, GLS) oder die Maximum-Likeliho- od (ML)-Methode zur Schätzung der Parameter eingesetzt werden. Die ML-Methode verlangt multivariat-normalverteilte Variablen, während die ULS- und GLS-Schätzme- thoden weniger restriktiv sind. Mit der neuesten Version LISREL VII können auch verteilungsfreie Schätzer ermittelt werden (jöreskog&Sörbom). Das Schätzproblem der ML-Schätzung in LISREL besteht darin, über den Parametervektor 7t (die unbenannten Parameter der acht LISREL-Matrizen) die Kovarianzmatrix X zu schätzen, die mit größter Wahrscheinlichkeit die empirische Kovarianzmatrix der Daten S erzeugt hat. Bei Annahme einer Wishartverteilung von S erfolgt die Schätzung über die iterative Minimierung der Funktion
LISREL

wobei tr die Spur einer Matrix angibt. Zur Beurteilung der Modellanpassung liefert LISREL dem Benutzer Fit-Maße und Teststatistiken (Konfirmatorische Faktorenanalyse). Zur Gesamtmodellprüfung kann im Fall der ML- oder GLS-Schätzung ein Chi2-T est eingesetzt werden. LISREL berechnet dabei einen modellspezifischen Wahrscheinlichkeitswert p für den Fehler erster Art (Ablehnung eines richtigen Modells), p sollte größer als eine Signifikanzschwelle von a= .10 sein. Die Teststatistik ist nur valide bei normalverteilten Daten, Analyse von Kovarianzmatrizen und angemessen großen Stichproben. Die Schätzung einer Gütefunktion kann über Hilfsverfahren erfolgen (Sa- torra & Saris). Ansonsten sollte die Statistik als Fitindex interpretiert oder zur Beurteilung alternativer Modellhypothesen als Chi2-Differenztest eingesetzt werden. Für explorative Studien liegt ein Modifikationsindex vor, der angibt, um wieviel sich die Teststatistik verbessert, wird ein weiterer Parameter geschätzt. Problematisch bei der Anwendung des Chi2- Tests ist seine Sensitivität gegenüber der Stichprobengröße. Deshalb ist es ratsam, mehrere ergänzende Fitindices nebeneinander zur Modellevaluation zu verwenden, etwa den Incremental-Fit-Index. Die Fitindices, Angaben über Standardfehler der Parameter und Residualvarianzen lassen eine verläßliche Aussage über die Validität eines geschätzten Modells zu. LISREL kann flexibel zur Spezifikation und Test vieler Modelltypen eingesetzt werden, z. B. Modelle der konfirmatorischen Faktorenanalyse zur Validierung; zweistufige konfirmatorische Faktormodelle; Kausalmodelle für die Ein- und Mehrgruppen- analyse; Zeitreihen- und Panelanalysen mit autokorrelierten Residuen; Modelle für höhere Produktmomente und der Test von Mittelwertstrukturen auf der Ebene der Faktoren. Für die Anwender entstehen Probleme dadurch, dass das Programm auch nicht zulässige Lösungen erzeugt (z.B. negative Varianzen). Dazu besteht die Möglichkeit, dass lokal unteridentifizierte Substrukturen in den Kausalmodellen auftreten können, die nur schwer aufzudecken sind (Identifikation). LISREL VII liegt vor als alleinstehendes Programm, als Supplement von SPSS(X) für den Großcomputer oder auch als PC-Version.

Literatur: Hildebrandt, L., Konfirmatorische Analysen von Modellen des Konsumentenverhaltens, Berlin 1983.Jöreskog,K. G., LISREL VI. Analysis of Linear Structural Relationships by the Method of Maximum Likelihood. User’s Guide, Mooresville, 2. Aufl., Indiana, Scientific Software, Inc. 1985. Long, S.J., Covariance Structure Models. An Introduction to LISREL, Sage Publications, Beverly Hills (CA), in: 1983.Satorra, A.; Saris, W., Power of the Likelihood Ratio Test in Covariance Structure Analysis, in: Psvchometri- ka, Vol. 50, No. 1, (1985), S. 83-90.

Vorhergehender Fachbegriff: liquidity trap | Nächster Fachbegriff: List of Messurement

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Landwirtschafts- und Verkehrs-Rechtsschutz | Fabrikhierarchie | Deckungsumsatz

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer