Ökonometrie

befasst sich mit der Quantifizierung und empirischen Überprüfung theoretischer Hypothesen und erlaubt Prognosen ökonomischer Variablen sowie Modellrechnungen (Simulationen) zu wirtschafts- und sozialpolitischen Alternativen im ökonomischen Kreislaufzusammenhang und in bezug auf individuelle Verhaltensweisen. 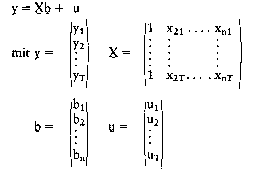Seit Gründung der Econo- metric Society 1931 ist die Verknüpfung von mathematischer Wirtschaftstheorie, Wirtschaftsstatistik und statistischer Schätz- und Testtheorie zu einer Synthese als das anspruchsvolle Programm der Ökonometrie formuliert worden. Bei der ökonometrischen Modellbildung sind folgende Schritte zu unterscheiden: • Spezifikation des Modells, • Schätzung, • Prüfung der ökonometrischen Struktur, • Bewertung der Ergebnisse.

Ziel der Spezifikation ist die Formulierung eines Modells in mathematischer Form. Dazu werden die im Rahmen der Wirtschaftstheorie entwickelten Hypothesen herangezogen und im Hinblick auf ihren Beitrag zur Lösung einer konkreten Problemstellung beurteilt. Es sind die wichtigsten Variablen, die in den Gleichungen berücksichtigt werden sollen, auszuwählen; ebenfalls ist die Funktionsform zu bestimmen (linear bzw. nichtlinear). Entsprechend der inhaltlichen Fragestellung werden makro- oder mikroökonomische Modelle (Mikroökonometrie) verwendet. In der zweiten Phase werden die Parameter (Koeffizienten) der Gleichungen, z.B. Multiplikatoren, Elastizitäten usw., durch Schätzung mit Hilfe bestimmter Methoden (Methode der kleinsten Quadrate, Maximum-Likelihood- Methode) quantitativ bestimmt. Die nunmehr ermittelte ökonometrische Struktur wird im Hinblick auf Qualitätskriterien überprüft. So sind Tests der ökonometrischen Modellannahmen (z.B. auf Autokorrelation oder Heteroskedastizität) und Parametertests (z.B. Signifikanz-Tests oder Struktur- bruchtests) durchzuführen. Schliesslich sind ökonomische Plausibilitätstests notwendig, die dazu dienen, die Vorzeichen und die Grössenordnungen der Parameter zu überprüfen. Die Bewertung der Ergebnisse ist nur in bezug auf die zugrunde liegende Problemstellung möglich. Ziel der ökonometrischen Modellbildung sind dabei letztlich Erklärung und Prognose wirtschaftlicher Entwicklungsprozesse. Literatur: Intriligator, M. D., Econometric Models, Techniques and Applications, Amsterdam, Oxford 1978. Judge, G. GJGriffiths, W EJHill, R. CJLee, T. CJLütkepohl, H., Introduction to the Theory and Practice of Econometrics, 2. Aufl., New York 1988, Schneeweiss, H., Ökonometrie, 4. Aufl., Heidelberg 1990. Hübler, O., Ökonometrie, Stuttgart, New York 1989.

Zweig der Volkswirtschaftslehre, der die ökonomische Theorie zu quantifizieren und mit der empirischen Wirtschaftsforschung zu verbinden versucht. Die Ökonometrie stellt eine Synthese aus mathematischer Wirtschaftstheorie und Methoden der Wirtschaftsstatistik dar und will nicht nur Aussagen über die Wirkungsrichtung bestimmter ökonomischer Variablen machen, sondern genauere, numerisch quantifizierbare Aussagen über ökonomische Einflüsse bzw. die wirtschaftlichen Auswirkungen politischer Maßnahmen treffen. Ziel der Ökonometrie ist es, auf der Basis empirisch gewonnener Daten ökonomische Theorien zu modifizieren, abzusichern oder auch zu verwerfen und insbesondere mit in der Realität bewährten Modellen Prognosen und Simulationen zu erstellen. Die Vorgehensweise der Ökonometrie lässt sich dabei folgendermaßen charakterisieren:
1. Spezifikation eines Modells,
2. Auswahl oder Erhebung geeigneter Daten für die ausgewählten Variablen,
3. Schätzung der Parameter mit anschließender Überprüfung hinsichtlich Plausibilität und Güte sowie
4. inhaltliche Interpretation und Auswertung der Ergebnisse.

In der Wirtschaftssoziologie: Bereich der Wirtschaftswissenschaft, dessen Aufgaben in der Messung wirtschaftlicher Sachverhalte und der empirischen Überprüfung ökonomischer Theorien bestehen. Die Ö. besteht heute in einer engen Verknüpfung von Statistik und Modellen der mathematischen Wirtschaftsforschung. Eine Reihe von Forschungsmethoden, die heute auch in der Soziologie benutzt werden, so Regressionsanalyse, Schätzverfahren, Zeitreihenanalyse, verdanken ihren Ausbau der Ö.

1. Charakterisierung Ökonometrie ist ein Teilgebiet der Wirtschaftswissenschaften, das Beziehungen zwischen ökonomischen Variablen in funktionaler Form bestimmen will. Insofern stellt die Ökonometrie eine Verbindung her zwischen ökonomischen Fragestellungen und hochentwickelten statistischen Methoden, die teilweise den Einsatz der EDV erfordern. Ist ein theoretisch fundierter Zusammenhang entdeckt, wird er mit empirischen Daten geprüft und konkretisiert.
2. Geschichte Die Ökonometrie entstand als eigenständige Disziplin im Jahre 1930 durch die Gründung der „Econometric Society” in Cleveland, Ohio. Seitdem hat sie ständig an Bedeutung zugenommen. Bald schon zeigte sich, dass die statistischen Methoden zur Lösung der sehr speziellen Problemstellungen nicht ausreichten, so dass in der Folgezeit filr die Weiterentwicklung der Statistik wesentliche Impulse von der Ökonometrie ausgingen.
3. Ökonomisches Modell Zur quantitativen Analyse der Zusammenhangsstruktur ökonomischer Variablen xi „.., setzt man ein Gleichungssystem an: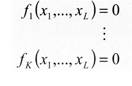

Dabei ist zunächst zu entscheiden, welche Variablen durch das Modell erklärt werden sollen (die sogenannten endogenen Variablen) und welche Variablen als erklärende auftreten (die sogenannten exogenen Variablen), die also ihre Bestimmung ausserhalb des Modellzusammenhangs haben. Variablen mit zeitlicher Dimension können dabei auf den Modellzeitpunkt t bezogen verzögert (Zeiten t — 1, t — 2,... ) oder unverzögert (Zeit t) eingehen. Es ist üblich, alle exogenen Variablen und die ver zögerten endogenen Variablen unter dem Begriff der vorherbestimmten Variablen zusammenzufassen. Die unverzögerten endogenen Variablen werden dann als gemeinsam abhängige Variablen bezeichnet. Da ein ökonomisches Modell i.A. nicht alle Einfluss nehmenden Grössen erfasst und Beobachtungen von Variablen immer mit einer gewissen Unschärfe erfolgen, kann ein Modell die Realität nur unzureichend abbilden. Die Modellgleichungen weisen somit eine zufällige Abweichung U auf: fax, ,..., x, )+ Uk = 0 für k= K . Mit dieser stochastischen Korrektur, die man auch Störterm oder Residuum nennt, ist der Übergang vom ökonomischen zum ökonometrischen Modell vollzogen.
4. Typen ökonometrischer Modelle Zunächst lassen sich Modelle nach der ökonomischen Zielsetzung unterscheiden. Während Erklärungsmodelle auf die Analyse ökonomischer Strukturen ausgerichtet sind, dienen Prognosemodelle der Vorhersage bestimmter endogener Variablen. Die wesentlichen Unterscheidungskriterien zur Modellabgrenzung sind aber nicht ökonomischen Ursprungs sondern rein formaler Art. Entsprechend der Anzahl K der Gleichungen spricht man von Eingleichungsmodellen (K = 1 ) oder Mehrgleichungsmodellen (K > 1). Dabei können sich in Mehrgleichungsmodellen die gemeinsam abhängigen Variablen gegenseitig beeinflussen (interdependente Modelle) oder nicht (rekursive Modelle oder Modelle mit unverbundenen Gleichungen). Sind alle endogenen Variablen unverzögert, liegt ein statisches Modell vor; dagegen nennt man ein Modell mit verzögerten endogenen Variablen dynamisch. Nach dem Funktionstyp der Modellgleichungen unterscheidet man lineare und nicht-lineare ökonometrische Modelle: Linear ist ein Modell, wenn sämtliche Gleichungen sowohl bzgl. der Variablen als auch bzgl. der Parameter linear sind. Modelle, die in den Parametern linear, aber nicht-linear in den Variablen sind, können durch die Definition neuer Variablen in lineare transformiert werden: So wird z.B. aus der Modellgleichung eines Polynoms y = sso + ss,x + ,62x2 + ss3x3 durch Transformation x, = x, x, = x2,x3 = x3 die lineare Gleichung y = ss0 + ss,x, +ss2x2ss3X3. Aber auch Modelle, die sowohl in den Parametern als auch in den Variablen nicht-linear sind, lassen sich häufig linearisieren. Ein Beispiel hierfür ist die Exponentialgleichung y = a•exp(6/x), die durch Logarithmieren in die lineare Form v = a + bu mit v = ln y, a = in a, b = ss,x =14 übergeht. Weiter werden Querschnitts- und Zeitreihenmodelle unterschieden, wenn die Beobachtungen entsprechenden Ursprungs sind. Das letzte Kriterium betrifft die Fehlspezifikation des Modells: Sind diese allein auf den Erklärungsansatz der Gleichungen zurückzuführen, so handelt es sich um ein sogenanntes Modell mit Fehlern in den Gleichungen; können dagegen die Variablen nicht genau beobachtet werden, liegt ein sogenanntes Modell mit Fehlern in den Variablen vor.
5. Eingleichungsmodelle Setzt man in das ökonomische Modell y = /30 + ss,x, +•••+ gix,,,f für die erklärenden Variablen N Beobachtungen xn •• xMn (n = 1, , N) ein, so erhält man ein lineares Modell der Ökonometrie: 1,,•,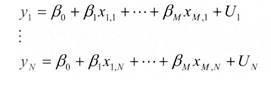

Dabei gleichen die Residuen U1,...,UN die zufälligen Abweichungen des Erklärungsansatzes zur y-Variablen aus, wobei E(U1) = = E(UN) = 0 vorausgesetzt wird. Mit der Design-Matrix X den Beobachtungen (x.„ ) , dem Parametervektor p=(ss0,...,xf)T, dem Vektor der Residuen u = (u„ , UN )T und dem Vektor der erklärten Variaben y = (yi, YN )T schreibt sich das Modell in Matrixform: y=X•ss+U Sind sämtliche Residuen unkorreliert mit gleicher Varianz 62 > 0, so ist 621 (I = Einheitsmatrix) die Kovarianzmatrix von y , und man spricht von einem einfachen linearen Modell (ELM). Hat die Kovarianzmatrix von y dagegen die Form 62V mit unbekanntem Parameter 62 und bekannter symmetrischer Matrix V , liegt ein verallgemeinertes lineares Modell (VLM) vor. a) Schätzverfahren Sind Realisierungen y des Modells bekannt, erfolgt die Bestimmung der unbekannten Parameter mit der Methode der kleinsten Quadrate, wenn die Verteilung der Residuen vollständig unbekannt ist, und mit dem Maximum Likelihood Verfahren, wenn die Verteilungsklasse bekannt ist. Sind die Residualgrössen normalverteilt, liefern beide Verfahren für 13 das gleiche Ergebnis: lieLm = (XTX)-STY im einfachen linearen Modell (auch Gauss-Schätzer oder OLSE = Ordinary Least Squares Estimator genannt) und YVLM = (xTv-\'X)\'xTv-ty im verallgemeinerten linearen Modell (auch Aitken-Schätzer oder GLSE=Generalized Least Squares Estimator genannt). Sowohl PELM als auch
3. sind erwartungstreu mit minimaler Varianz in der Klasse der linearen Schätzverfahren (Satz von Gauss-Markoff). Bei normalverteilten Residuen haben ELM und   sogar minimale Varianz in der Klasse aller erwartungstreuen Schätzverfahren. EineYVLM erwartungstreue Schätzung für 62 ergibt sich dann zu N - M 1                          T VLMN - M XKLM ) Vy—XPVLM) Auch hier haben bei normalverteilten Residuen beide Schätzverfahren minimale Varianz in der Klasse der erwartungstreuen Schätzverfahren. Zu Bereichsschätzverfahren und Testverfahren wird auf die angegebene Literatur verwiesen. 21 ELM = - xiiELM)T(Y. XbELM b) Friktionen Bei der Modellierung können mehrere Probleme auftreten.
(1) Identifizierbarkeit: Gibt es zwei ver schiedene Parametervektoren III und 132, für die aber die Verteilungen von Y(I31) und Y(I)2) gleich sind, so ist ss im linearen Modell nicht identifizierbar bzw. gleichbedeutend: ss ist nicht linear schätzbar. Identifizierbarkeit kann aber durch zusätzliche Beobachtungen erreicht werden.
(2) Multikolineari tät: In diesem Fall gibt es lineare Abhängigkeiten zwischen den (Beobachtungen der) erklärenden Variablen x            xm X. Damit ist die Matrix XTX nicht invertierbar, und OLSE bzw. GLSE können nicht berechnet werden. Eine Reduktion der Parameter bietet hier die Möglichkeit zur Korrektur.
(3) Autokorrelation: Zwischen den Residuen bestehen Abhängigkeiten, d.h. E(UkUn) # 0 für k n ist möglich. Lassen sich diese durch einen autoregressiven Prozess
1. Ordnung (mit ipi < 1, e„ = N(0; cre2), E(ek, ) = 0 für k # n) modellieren, gestaltet sich die Kovarianzmatrix von y besonders einfach und kann aus den Daten geschätzt werden.
(4) Heteroskedastie: Im einfachen linearen Modell ist die Bedingung gleicher Varianzen der Residuen nicht erfüllt. Da für jeden Parameter un i.A. nur eine Beobachtung vorliegt, sind die Möglichkeiten der Parameterbestimmung stark eingeschränkt. Einen beachtenswerten Ansatz zur allgemeinen Schätzung von Varianzkomponenten stellt C. R. Rao mit dem MINQUE-Verfahren vor (Minimum Norm Quadratic Estimator).
6. Mehrgleichungsmodelle Wie bei den Eingleichungsmodellen wird auch hier meist Linearität in den Parametern vorausgesetzt. Zu deren Bestimmung finden wieder die Methode der kleinsten Quadrate und — falls das Verteilungsgesetz der Störvariablen bekannt ist — die Maximum Likelihood Methode Anwendung. Zu den — teilweise recht aufwendigen — Details wird auf die angegebene Literatur verwiesen. Hinweis Zu den angrenzenden Wissensgebieten siehe   Finanzmathematik,   Operation Research,   Optimierungsmodelle, mathematische,   Portfoliomanagement,   Statistik,   Wirtschaftsmathematik.

Literatur: Poddig, Th., Dichtl, H., Petersmeier, K.: Statistik, Ökonometrie, Optimierung, Methoden und ihre praktischen Anwendungen in Finanzanalyse und Portfoliomanagement, Uhlenbruch Verlag, Bad Soden/Ts. 2003; Seber, G.A.F., Wild, C.J.: Nonlinear Regression, John Wiley, New York 1989; Frohn, J.: Grundausbildung in Ökonometrie, de Gruyter, Berlin 1995; Schneeweiss, H.: Ökonometrie, Physik-Verlag, Heidelberg 1990; Hübler,
0. : Ökonometrie, Gustav Fischer Verlag, Stuttgart 1989; Rao, R.C.: Linear Statistical Inference and its Applications, John Wiley 1973.

Vorhergehender Fachbegriff: Ökomanagement | Nächster Fachbegriff: Ökonometrie

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Äquivalenzziffernkalkulationen | Hängeposition | Vermögenslage

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer