hypergeometrische Verteilung

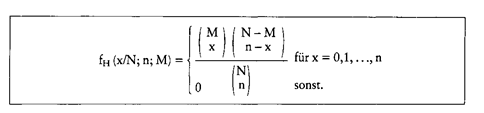Wahrscheinlichkeitsverteilung, die z.B. im Urnenmodell ohne Zurücklegen entsteht: Aus einer Urne, die mit M schwarzen und N-M weissen Kugeln, die also insgesamt mit N Kugeln gefüllt ist, wird eine Zufallsstichprobe im Umfang n "ohne Zurücklegen" gezogen. Die Wahrscheinlichkeit, dass sich unter den n gezogenen Kugeln genau x schwarze befinden, wird durch die Wahrscheinlich keitsfunktion der hypergeometrischen Verteilung gegeben (vgl. Formel). Die Form der hypergeometrischen Verteilung wird durch die konkreten numerischen Werte der Parameter N, n und M bestimmt. Abhängig von den konkreten Werten der Parameter N, n und M können als Approximationen die Binomialverteilung, die Poissonverteilung und/oder die Normalverteilung Verwendung finden. Literatur: Bleymüller, JJ Gehlert, GJGülicher, H., Statistik für Wirtschaftswissenschaftler, 8. Aufl., München 1992.

Eine diskrete theoretische Verteilung der mathematischen Statistik für die Auswahl ohne Zurücklegen. Entnimmt man aus der Grundgesamtheit mit N Elementen eine - Stichprobe von n Elementen, so wird die Wahrscheinlichkeit, genau m Elemente mit der Ausprägung M (bei insgesamt M Elementen mit der einen und N — M Elementen mit der anderen Ausprägung in der Grundgesamtheit) zu ziehen, durch die Wahrscheinlichkeitsfunktion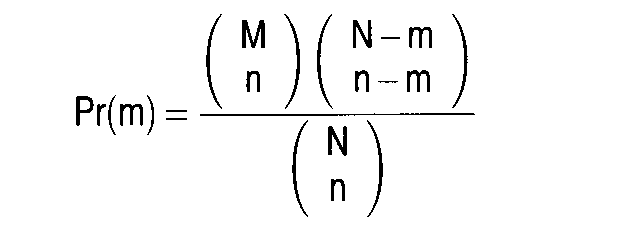

gegeben. Eine hypergeometrische Verteilung ergibt sich, wenn man m sukzessive alle möglichen Werte von 0 bis n durchlaufen läßt. Bei großem Umfang der Grundgesamtheit und kleinem Auswahlsatz unterscheidet sich die hypergeometrische Verteilung von der Binomialverteilung kaum und geht ebenso wie diese für große n und sehr große N in die Normalverteilung über. Der Mittelwert der hypergeometrischen Funktion lautet: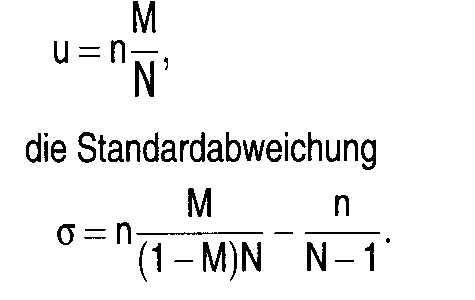

hypergeometrische Verteilung

Als Signifikanztest wird die hypergeometrische Verteilung auch als Fisher-Yates-Test bezeichnet.

Vorhergehender Fachbegriff: Hypercube | Nächster Fachbegriff: Hyperinflation

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Investitionskartell | logrolling | ASIA Invest

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer