Monopolgradtheorie

Verteilungstheorie

sucht die Einkommensverteilung aus Machtfaktoren zu erklären. Bleibt man im Rahmen der Neoklassischen Theorie, einschl. Gewinnmaximierung und Geltung des Grenzproduktivitätssatzes, dann bietet sich zur Kennzeichnung von »Macht« der auf Abba P. LERNER zurückgehende Begriff des Monopolgrades an: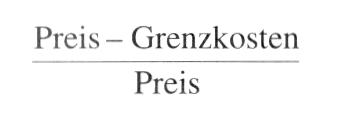
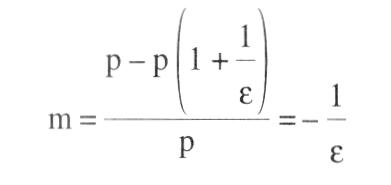Monopolgradtheorie

Da im Gewinnmaximum die Grenzkosten gleich dem Grenzumsatz sind, und der Ausdruck für den Grenzumsatz nach der AMOROSO-ROBINSON-Bedingung p+p/e lautet, wobei p den Produktpreis und e die Preiselastizität der Nachfrage kennzeichnet, läßt sich der LERNERsche Monopolgrad dann ausdrücken durch
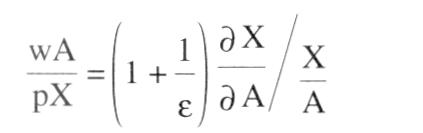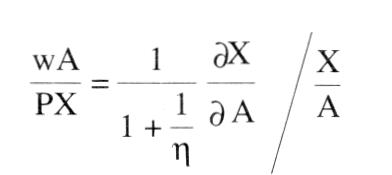Monopolgradtheorie

Bei einer normal geneigten Nachfragekurve auf dem Produktmarkt ist e negativ und damit der Monopolgrad positiv. Die erste Bedingung des Gewinnmaximums lautet: (w = Geldlohn, A = Arbeitsmenge, X = Produktmenge, dX/dA = Grenzproduktivität der Arbeit). Der Lohnanteil ist:
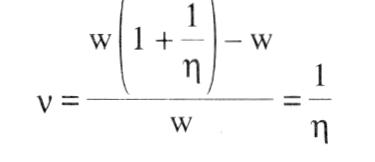Monopolgradtheorie

Da e negativ ist, fällt der Lohnanteil geringer aus als bei vollständiger Konkurrenz. In entsprechender Weise wie der Monopolgrad auf dem Produktmarkt läßt sich für den Arbeitsmarkt ein Monopsongrad formulieren B ist die Elastizität der Bezugskurve für Arbeit. Der Lohnanteil wäre in diesem Fall: Wegen 11 > 0 ist der Lohnanteil im Fall eines Monopsons auf dem Arbeitsmarkt größer als bei vollständiger Konkurrenz. Insbes. hinsichtlich des Produktmarktes bereitet die Übertragung des LERNER-sehen Monopolgrads auf die Gesamtwirtschaft Schwierigkeiten. Die gesamtwirtschaftliche Nachfragekurve kann nicht als Aggregation der einzelwirtschaftlichen Nachfragekurven angesehen werden (selbst nicht im Ein-Produkt-Modell), weil mit Hilfe der gesamtwirtschaftlichen Nachfragekurve die Einkommensgröße, die bei den einzelwirtschaftlichen Nachfragekurven als gegeben vorausgesetzt wird, erst zu bestimmen ist. Versucht man, den wechselnden Gesamteinkommensgrößen in den individuellen Preiselastizitäten Rechnung zu tragen, so zeigt sich, dass diese von der Einkommensverteilung abhängen, die ihrerseits erst bestimmt werden soll. Die mangelnde Übertragbarkeit des LERNERschen Monopolgradbegriffs auf die Gesamtwirtschaft bewirkt, dass die gesamtwirtschaftliche Monopolgradtheorie i.d.R. von einer autonomen Preisbestimmung und ggf. auch von einer autonomen Lohnbestimmung ausgeht. Das Gewinnmaximierungsprinzip wird aufgegeben. Es wird ein Zuschlag auf die variablen Durchschnittskosten erhoben, der durch die Zielsetzungen, die Marktstellung und die Verhaltensweisen der Unternehmen bestimmt wird (Zuschlagskalkulation oder mark-up pricing). Für die Gesamtwirtschaft mit Y, als realem Sozialprodukt ergibt sich unter der Annahme, dass alle variablen Kosten auf Lohnkosten zurückgeführt werden können:
Monopolgradtheorie

z ist hierbei der autonom bestimmte prozentuale Zuschlag. Daraus ergibt sich die Lohnquote: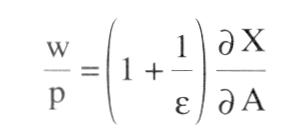
Monopolgradtheorie

und die Profitquote. Dies ist nichts anderes als der Monopolgrad, wenn er durch definiert wird. Statt dessen können wir auch schreiben Mit dem Zuschlag sind somit die Einkommensanteile bestimmt. Gleichgültig ist es hierbei, ob die Differenz zwischen Preis und durchschnittlichen Lohnkosten durch eine Heraufsetzung des Preises oder durch Niedrighaltung der Lohnkosten zustande gekommen ist. Im Monopolgradmodell von Michal KALECKI sind neben den Lohnkosten noch die Rohstoffkosten in die variablen Kosten einbezogen (KALECKI-Verteilungstheorie). Wichtig ist die Verwendung der mit Hilfe des Monopolgrads definierten Einkommensverteilung in gesamtwirtschaftlichen Modellen. Ein einfaches Beispiel bietet die Zusammenführung mit einem Zweiklassen-Modell nach Nicholas KALDOR, in dem Sparquoten von Lohn-und Profitempfängern unterschieden werden. Für sich allein genommen wird entweder die Verteilung bei gegebener Investitionsquote oder die Investitionsquote bei gegebener Verteilung bestimmt. Wegen I /y =z/i.„ wird es aber nun möglich, in der KALDOR-Gleichung die Investitionsquote zu ermitteln bzw. bei gegebener Investitionshöhe die Volkseinkommensgröße. Verwendet wird der Monopolgrad ebenfalls in der Preisänderungsgleichung von Modellen zur PHILLIPS-Kurve. Führt man außerdem in die Lohnveränderungsgleichung gewerkschaftliche Machteinflüsse mit ein, ist der Übergang zu einem Verteilungskampfmodell beschritten. Es ist zu prüfen, ob das System zu steady state growth hintendiert und ob diese Lösung stabil ist. Die steady-state-Lösung ist dadurch gekennzeichnet, dass keine Umverteilung zwischen Arbeitnehmern und Unternehmen stattfindet, dass also die Lohnsteigerung der erwarteten Preissteigerung zuzüglich der Produktivitätssteigerung entspricht. Üblich ist es auch, die Verteilung in der Neuen Makroökonomik (Ungleichgewichtsmodelle oder Modelle des temporären Gleichgewichts mit Mengenrationierung) durch Machteinflüsse zu erklären, die in der Lage der gesamtwirtschaftlichen Angebotskurve zum Ausdruck kommt. Zu Verteilungskampfmodellen werden solche Modelle, indem man von unterschiedlichen Vorstellungen der Arbeitnehmer und Arbeitgeber hinsichtlich des anzustrebenden Reallohnes ausgeht und die Versuche jeder Seite, ihre Reallohnvorstellung zu realisieren bzw. sich den Vostellungen der anderen Seite anzunähern, als Prozess darstellt. Literatur: Bartmann, H. (1981). Blumle, G. (1975)

Vorhergehender Fachbegriff: Monopolgrad | Nächster Fachbegriff: monopolistische Konkurrenz

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Bonifikation | Stabilisierungspolitik | Innerbetrieblicher Verrechnungspreis

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer